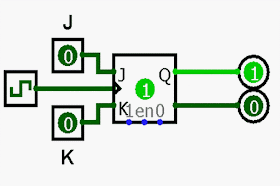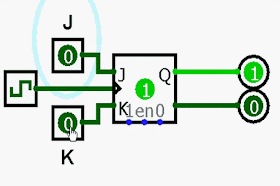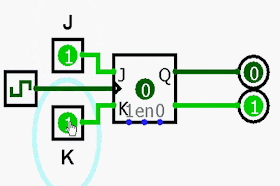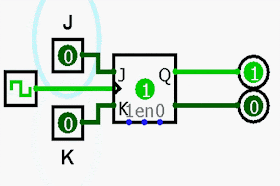
1. Monte o circuito e explique o funcionamento de um contador síncrono decrescente de módulo 10.
Resolução:
Resolução:
 |
| Contador decrescente módulo 10 |
OU
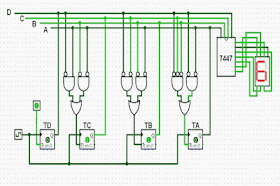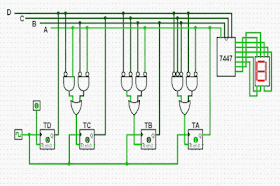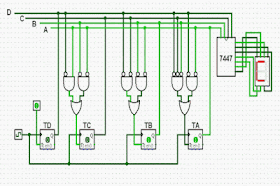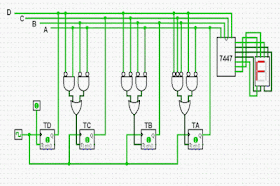 |
| Contador decrescente módulo 10 |
 |
| Contador síncrono decrescente JK |
CLIQUE AQUI para fazer o download do arquivo feito no Logisim
2. As formas de onda de entrada mostradas na figura 2 são aplicadas num somador de 2 bits. Determine as formas de onda para a soma e o carry de saída em relação às entradas construindo o diagrama de temporização.
Resolução:
3. Projete um circuito lógico com o DEMUX que tem a capacidade de indicar se um número pertence aos números primos. Admita que você tenha disponível apenas DEMUX com oito saídas e portas OU de três entradas. O conjunto a ser analisado é composto de números inteiros entre 0 e 31.
Resolução:
4. Converta o código Gray 1111 para binário.
Resolução:
 |
| Circuito conversor de código gray para binário |
5. Para o FF da figura abaixo, desenhe a forma de onda na saída em função dos sinais aplicados.
Resolução: