Lista de exercício 2 CCA

1. Sobre um resistor de 2K2 aplica-se uma tensão VRMS =110V ; f = 60Hz. 

a)Calcule a intensidade da corrente IRMS. 

Resolução:

Vrms = V / √2 

V = 110 . √2 = 155,56 [V]

I = V / R = 155,56 / 2200 = 0,07 [A]

Irms = 0,07 / √2 = 0,05 [A] = 50 [mA]

2. Um resistor de 50 Ω é ligado a uma fonte CA de VM =300V e f=100Hz. Calcule a intensidade da corrente medida por um amperímetro que está ligado em série com a carga consumidora.

Resolução:

V = 300 / √2 = 212,13 [V]

i = V / R= 212,13 / 50= 4,24 [A]

3. No exercício anterior, pretende-se substituir a fonte CA por uma CC que produza a mesma dissipação de energia no resistor. Que valor deverá ter a tensão dessa fonte?

Resolução:

Vrms = Vp / √2 = 300 / √2 = 212,13 [V]

4. Uma fonte gera f.e.m. e = 60sen 500t (V) e possui resistência interna r =2 Ω . Calcule o valor eficaz da corrente e da tensão no resistor de 1kW / 220V ligado a ela.

Resolução:

Vrms = Vp / √2 = 60 / √2 = 42,43 [V]

R= V² / P = 220² / 1000 = 48,4 [Ω]

Irms = V / Req = 42,43 / (2 + 48,4) = 0,84 [A]

V= R . i = 48,4 . 0,84 = 40,74 [V]

5. Calcule a reatância de um capacitor de 1nF à frequência de 50 Hz, 60 Hz, 1 KHz e 1 MHz

Resolução:

para 50 Hz

Xc = 1 / 2.π.50.1/10⁹ = 3183098,86 [Ω]

para 60 Hz

Xc = 1 / 2.π.60.1/10⁹ = 2652582,38 [Ω]

para 1 KHz

Xc = 1 / 2.π.1000.1/10⁹ = 159154,94 [Ω]

para 1 MHz

Xc = 1 / 2.π.10⁶.1/10⁹ = 159,15 [Ω]

6. Esboce um gráfico I= f(f) para um capacitor de 1μF alimentado com 10V, com frequência variável de 0 a ∞. Utilize os eixos ao lado.

Resolução:

para 55 KHz 

XL= 2.π.55/10³ = 0,35 [Ω]

7. Um capacitor de 77μF está conectado numa rede de CA, onde temos Vmáx= 170V e f= 50 Hz. Determine o valor da corrente medida por um amperímetro ligado em série com o circuito.

Resolução:

Xc = 1/ 2.π.f.c = 1 / 2.π.50.77x10^-6

Xc = 41,34 [Ω]

Vrms = 170 / √2 = 120,2 [V]

I = V/R = 120,2 / 41,34 = 2,91 [A]

8. Um capacitor de 10μF está ligado a uma fonte de tensão v= 300sen(ωt), sendo f= 60 Hz. Calcule o valor instantâneo da corrente em t= 2ms.

Resolução:

V = 300.sen(2 . 180 . 2 / 1000) = 3,77 [V]

Xc = 1/ 2.π.f.c = 1 / 2.π.60.10x10^-6  = 4,63 [Ω]

Irms = V / R = 3,77 / 4,63 = 0,814 [A]

9. Um capacitor de placas planas e paralelas de 5cm x 80cm cada, com um dielétrico de 0,2mm de espessura e K= 500 é ligado a uma fonte de 127V / 50Hz. Considerando-o como capacitor puro, calcule o valor eficaz da corrente que circulará.

Resolução:

Xc = 1 / 2.π.50.885/10⁹  = 3596,72 [Ω]

I = V/R = 127 / 3596,72 = 35,31 [mA]

10. Um capacitor de C= 42μF é ligado a uma fonte de 220V / 60Hz. Calcule o valor da corrente.

Resolução:

Xc = 1 / 2.π.60.42/10⁹  = 63156,72 [Ω]

i = V/R = 220 / 63156,72 = 3,48 [mA]

11. Calcule a reatância de um indutor de 1mH à frequência de 50 Hz, 60 Hz, 1 KHz e 1 MHz.

Resolução:

P/ 50 Hz

 L= 1/10³ H

XL= 2π.50.1/10³ = 0,314 [Ω]

P/ 60 Hz

XL= 2π.60.1/10³ = 0,377 [Ω]

P/ 1 KHz

XL= 2π.10³.1/10³ = 6,283 [Ω]

P/ 1 MHz

XL= 2π.10⁶/10³ = 6283,18 [Ω]

12. Por uma bobina de 7mH circula uma corrente (CA) de Imáx= 14,1A numa frequência de 50Hz. Determine o valor da tensão medida por um voltímetro ligado em paralelo com a bobina. 

Resolução:

XL= 2π.50.7/10³ = 2,2 [Ω]

V= Imax / √2 = 2,2 . 14,1 / √2 = 21,92 [V]

13. Um indutor puro de L=300mH é ligado a uma fonte de 127V / 50Hz. Calcule o valor da corrente medida por um amperímetro ligado em série com o indutor. 

Resolução:

XL=  2.π.50.300/10³ = 94,24 XL= [Ω]

I = V/R = 127 / 94,24 = 1,35 [A]

14. Se a frequência da fonte da questão anterior subir para 1 kHz, qual o novo valor da corrente?

Resolução:

XL= XL=  2.π.1000.300/10³ = 1884,95 [Ω]

I= V/XL = 127 / 1884,95 = 67,37 [mA]

15. Um indutor puro de 3H é alimentado com uma tensão máxima (tensão de pico) VM = 400V. Sabendo-se que a corrente varia de acordo com a senóide ao lado, determine o valor instantâneo da corrente quando a tensão está com o valor referente a 225° elétricos.

Resolução:

f= 1/T = 1/ (18,18/1000) = 55 Hz

V= 400.sen(2 . 180 . 55 . 11,36/1000 + 6) = 400.sen(2 . 180 . 55 . 11,36/1000 + 0) =  -282,48 [V]

I= V/R = V/XL= -282,48 / (2.π.55.3)= -0,272 [ A]

16. Dados os pares de expressões para tensões e correntes a seguir, determine se o dispositivo envolvido é um capacitor, um indutor ou um resistor e calcule os valores de C, L e R. 

a) V= 100sen (ωt + 40° ) e i= 20sen (ωt + 40° ) 

Resolução:

f= 1/T = 1/2.π = 0,16 Hz

V= 100.sen(2 . 180 + 40°) = 64,28 [V]

I= 20.sen(2 . 180 + 40°) = 12,85 [A]

R= V/I = 64,28 / 12,85 = 5[Ω]

b) V=1000 sen (377t + 10° ) e i= 5.sen (377t - 80° ) 

Resolução:

XL= 1000 /  5 = 200 [Ω]

XL= 2π.C.L

L= 200 / 377= 0,530 H

c) V= 500 sen (157t + 30° ) e i= 1 sen (157t + 120° ) 

Resolução:

V= Xc . I= 5[Ω]

C= 1/(157 . 5)= 12,74 μF

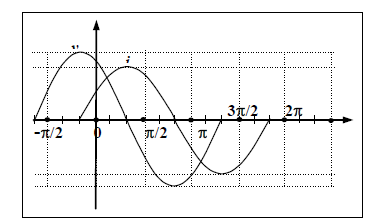
17. Num circuito puro alimentado por CA, a tensão e a corrente variam de acordo com as equações a seguir: i= 3.sen (ωt+300 ) e V= 2.sen (ωt - 600 ). Identifique o ângulo de defasagem entre a tensão e a corrente, represente estas grandezas no gráfico ao lado e diga que tipo de circuito se trata (carga resistiva, capacitiva ou indutiva).

Resolução:

φ= - 180° + 3 . 180° / 2 = 90°

φ=90° , i está adiantada de 90° em relação a v, carga capacitiva 

18. Em que frequência um indutor de 5 mH terá a mesma reatância de um capacitor de 0,1 μF?

Resolução:

Xc = XL

1/ 2π.f. 0,1/10⁶  = 2π.f. 5/10³

1/(2π)² . 0,1/10⁶ . 5/1000 = f ² 

f= 7,11 KHz

19. Num circuito puramente indutivo (gráfico representado ao lado) circula uma corrente i= 10 .sen(377t). Sabendo-se que a indutância do indutor vale 0,1 H, determine o valor máximo (valor de pico) da tensão

Resolução:

i = 10.sen(377t)

XL= 377 . 0,1= 37,7 [Ω]

V= R . I= XL . I = 37,7 . 10= 377 [V]

20. Refaça o problema anterior, considerando uma corrente i = 10sen(377t+300 ) e esboce as curvas de v e i no gráfico ao lado.

Resolução:

21. Faça novamente o problema 19, considerando que a corrente é i = 7.sen(377t -70° ) e esboce as curvas de v e i num novo gráfico. 

Resolução:

22. Num circuito puramente capacitivo (gráfico representado ao lado) é aplicada uma tensão V= 30sen 400t . Sabendo-se que a capacitância do capacitor vale 1 μF determine o o valor máximo (valor de pico) da corrente.

Resolução:

W  = 2π.f

400 = 2π.f

f = 63,66 Hz

C = 1 μF = 10^-6 F

Xc = 1 / 2π.f.C = 2500 [Ω]

i = V / /R = V / Xc = 30/2500 =0,012 [A] = 12 [mA]

23. A expressão para a corrente num capacitor de 100 μF é i = 40.sen(500t + 60° ). Determine a expressão senoidal (equação característica) para a tensão no capacitor.

Resolução:

Xc= 1/ω.c = 1/(500.100/10⁶ = 20 [Ω]

V= R . I= Xc . I = 20 . 40= 800 [V]

θ= 60° - 90°= -30°

V= 800.sen(500t - 30°)

24. São dadas a seguir expressões para a corrente em uma reatância indutiva de 20Ω. Qual é a expressão senoidal para a tensão em cada caso ? 

a) i = 5 sen(ωt +90°) i = 0,4.sen(ωt + 60° ) 

 

 Resolução:

i = 5sen(ωt)

Vp= XL . I= 20 . 5= 100 [V]

V= 100.sen(ωt - 90°)

i = 0,4.sen(ωt + 60°)

Vp= Xl . I= 20 . 0,4= 8 [V]

θ= 90° + 60°= 150°

V= 8.sen(ωt - 150°)

25. A seguir são apresentadas as expressões para a tensão aplicada a um capacitor de 0,5μF. Qual é a expressão para a corrente em cada caso ? 

a) v = 127,2 sen(754t)

Resolução:

Xc = 1 = W . C = 1 / 754 . 0,5 / 10⁶ = 2652,5 [Ω]

i = V / R = 127,2 / 2652,5 = 0,048 [A]

i = 0,048 . sen(745.t + 90°)

b)v = 100 sen (1600t-170° )

Resolução:

V= 100 . sen(1600.t - 170°)

Xc = 1 / (1600 . 0,5/10⁶) = 1250 [Ω]

i = V / R = V / Xc = 100 / 1250 = 0,08 [A]

θ = -170° + 90° = - 80°

i = 0,08 . sen(1600.t - 80°)