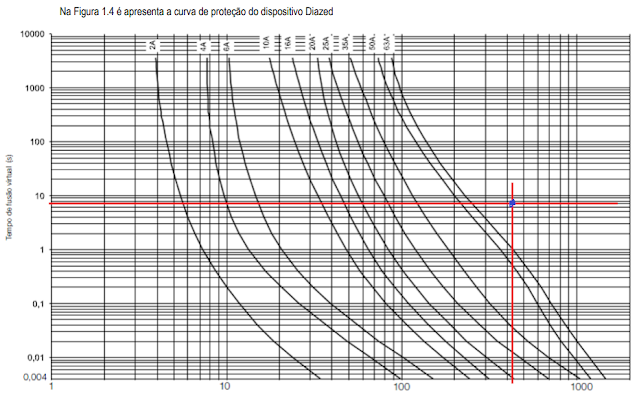
Lista de atividades para cálculos de seção dos condutores em motores elétricos :
1) Um motor indução trifásico de 15 cv com alimentação em 220V, 60 Hz, fator de
potência 0,85 e rendimento 0,9. A corrente de partida é seis vezes a nominal. Determine: corrente
nominal e de partida e a seção do cabo. Adotar Temperatura de 40°. Dois circuito no eletro duto.
Resolução:
Ic = In / Fca . Fct , onde:
Ic = Corrente corrigida
Ip = Corrente de partida
In = Corrente nominal (corrente de projeto)
Fca = Fator da correção de agrupamento
Fct = Fator da correção de temperatura
k = Multiplicador
In = Pmec . cv / √3. Vn . cos(θ). η = 15 . 736 / √3. 220 . 0,85 . 0,9
In = 37,87 [A]
k = Ip / In [A]
Ip = 6 . In = 6 . 37,87
Ip = 227,23 [A]
Ic = 37,87 / (1 . 0,87 )
Ic = 43,53 [A]
* Fator de correção:
Kagr = 0,80 → 2 circuitos fechados em eletroduto (tabela 3.5 item 1)
Temperatura ambiente: 40°C , isolamento PVC (Tabela 1.2) Ktemp = 0,87
Fator global
K = Kagr . Ktemp = 0,80 . 0,87 = 0,696
* Corrente requerido do cabo
Inec = In/K = 37,9 / 0,696 = 54,4
* Escolha da seção ( Cobre, PVC, em eletroduto )
10 mm² → ≈ 57A OK
16 mm² → ≈ 76A OK superdimensionado
* Seção recomendada segundo a NBR 5410 (Método B1/C)
3 # 10(10) mm² (Cobre PVC)
2) Um motor indução trifásico de 10 cv com alimentação em 220V, 60 Hz, fator de
potência 0,8 e rendimento 0,85. A corrente de partida é seis vezes a nominal. Determine: corrente
nominal e de partida e a seção do cabo. Adotar Temperatura de 35°. Três circuito no eletroduto.
Resolução:
In = 10 . 736 / ( √3 . 220 . 0,8 . 0,85 ) = 28,40 [A]
Ip = Ip / In
Ip = 6 . In = 6 . 28,40 = 170,43 [A]
Ic = In / Fca . Fct , onde:
Ic = Corrente corrigida
In = Corrente nominal (corrente de projeto)
Fca = Fator da correção de agrupamento
Fct = Fator da correção de temperatura
Ic = In / (1 . 0,87 ) = 28,40 / (1 . 0,87)
Ic = 32,64 [A]
* Fatores de Correção:
Kagr = 0,70 → Tabela 3.5 para 3 condutores
Ktemp = 0,94 → Tabela 1.2 para 35°C
K = 0,70 . 0,94 = 0,658
* Capacidade de condução mínima exigida
Inec = In / K = 28,4 / 0,658 = 43,2A
* Escolha da seção do cabo (Cobre, 70°C, PVC, em eletroduto )
10 mm² → ≈ 57A OK
16 mm² → ≈ 76A OK superdimensionado
* Seção recomendada para valores típicos da NBR 5410 (método B1/B2) a 30 °C antes dos fatores de correção.
3 # 10(10) mm² (Cobre PVC)
3) Um motor indução trifásico de 3 cv com alimentação em 220V, 60 Hz, fator de
potência 0,7 e rendimento 0,55. A corrente de partida é seis vezes a nominal. Determine: corrente
nominal e de partida e a seção do cabo. Adotar Temperatura de 45°. Quatro circuito no eletroduto.
Resolução:
In = Pmec . cv / √3. Vn . cos(θ). η
In = 3 . 736 / ( √3 . 220 . 0,7 . 0,55
In = 15,05 [A]
Ip = Ip / In
Ip = 6 . 15,05 = 90,30 [A]
* Fator de correção
Fc = 0,66 . 0,79 = 0,5214
* Corrente corrigida
Ic = In / Fc = 15,05 / 0,52,14 = 28,9A
* Seção do cabo
. Pela tabela da NBR 5410
Condutor de cobre, isolação PVC, método B1(eletroduto embutido), temperatura 30° para corrente 28,9A cabo = 3 # 6(6) mm²
4) Um motor indução trifásico de 2,5 cv com alimentação em 220V, 60 Hz, fator de
potência 0,6 e rendimento 0,5. A corrente de partida é seis vezes a nominal. Determine: corrente
nominal e de partida.
Resolução:
. P = 2,5 cv
. Tensão = 220 V(trifássico)
. Fator de potência = 0,6
. Rendimento ( η ) = 0,5
. Frequencia = 60 Hz
. Corrente de partida = 6 vezes a nominal
P = 2,5 . 736 = 1840 W
In = P / ( √3 . V . FP . n ) = 1840 / (√3 . 220 . 0,6 . 0,5) = 16,09 A
Corrente de partida
Ip = 6 . In = 6 . 16,09 = 96,54A
* Fator de correção
Fc = 0,79 . 0,66 = 0,5214
* Corrente corrigida
Ic = In / Fc = 16,09 / 0,5214 = 30,85A
* Seção do cabo
. Cabo de cobre isolação PVC método B1 em 30°C pela NBR 5410
3 # 6(6) mm²
5) Um motor indução trifásico de 100 cv com alimentação em 220V, 60 Hz, fator de
potência 0,92 e rendimento 0,85. A corrente de partida é seis vezes a nominal. Determine:
corrente nominal e de partida.
Resolução:
P = 100 . 736 = 73600 W
In = 73600 / ( √3 . 220 . 0,92 . 0,85) = 246,54A
Ip = 6 . 246,54 = 1479,2 A
* Fator de correção
. Tabela 1.2 para 45° isolação PVC
Ft = Fator térmico = 0,79
. Tabela 11
Para 4 circuitos no eletroduto item 1
Fa = Fator de agrupamento - 0,66
Fc = 0,79 . 0,66 = 0,5214
* Corrente corrigida
Ic = In / Fc = 246,54 / 0,5214 = 472,75 A
* Seção do cabo
. Para I = 472,75A seção do cabo de acordo com a NBR 5410
3 # 240(120) mm²
Alternativas para 3 # 240(120) mm²
. 2 condutores de 120 mm² por fase em paralelo
. 2 condutores de 150 mm² por fase
. 1 condutor de 240 mm² por fase