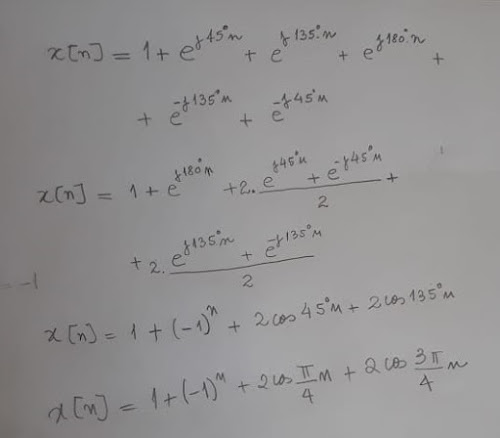Multiplexação por divisão de frequência no MATLAB

Código feito no Matlab

% test_orthogonality.m

% Verificar a ortogonalidade entre alguns sinais senoidais

% com diferentes frequências/fases

clear, clf

T=1.6; ND=1000; nn=0:ND; ts=0.002; tt=nn*ts; % Intervalo de tempo

Ts = 0.1; M = round(Ts/ts); %Período de amostragem em tempo contínuo/discreto

nns = [1:M:ND+1]; tts = (nns-1)*ts; % Índices e tempos de amostragem

ks = [1:4 3.9 4]; tds = [0 0 0.1 0.1 0 0.15]; % Frequências e atrasos

K = length(ks);

for i=1:K

k=ks(i); td=tds(i); x(i,:) = exp(j*2*pi*k*(tt-td)/T);

if i==K, x(K,:) = [x(K,[302:end]) x(K-3,[1:301])]; end

subplot(K,2,2*i-1), plot(tt,real(x(i,:))),

hold on, plot(tt([1 end]),[0 0],'k'), stem(tts,real(x(i,nns)),'.')

end

N = round(T/Ts); xn = x(:,nns(1:N));

xn*xn'/N % verificar ortogonalidade

Xk = fft(xn.').'; kk = 0:N-1;

for i=1:K, k=ks(i); td=tds(i); subplot(K,2,2*i), stem(kk,abs(Xk(i,:)),'.')end

Saída gerada no Matlab online

a) Encontre H(Z), faça diagrama de polos e zeros e indique a RDC

Resolução:

1.a)

b) Encontre a resposta ao impulso do sistema

Resolução:

c) Escreva a equação de diferença que caracteriza o sistema

Resolução:

d) O sistema é estável e causal ?

Resolução:

2) A entrada de um sistema LIT causal é x[n]=u[-n-1]+(1/2)ⁿ u[n]. A transformada Z da saída desse sistema é 𝑌(𝑧) = 

a) Determine H(z) e sua RDC

b) Qual a RDC para Y(z) ?

c) Determine y[n].

Resolução:

2.b)

2.c)

3) : Um sistema LIT tem resposta ao impulso definida por: 

Determine y[n], numericamente e graficamente, para x[n]= u[n]-u[n-4].

Resolução:

4)  Considere um sistema LIT que seja estável e para o qual H(z), a transformada Z da resposta ao impulso, seja dada por:

Suponha que x[n], a entrada do sistema, seja uma sequência degrau unitário.

a) Determine a saída y[n] calculando a convolução discreta de x[n] com h[n].

b) Determine a saída y[n] calculando a transformada inversa z de Y(z).

 

Resolução :

4.a)

4.b)

5)  Considere a figura abaixo onde se tem a associação em cascata de dois sistemas.

a) Esboce w[n] se x[n]=(-1)ⁿ u[n]. Determine também y[n].

b) b) Determine e esboce a resposta ao impulso total do sistema em cascata, isto é, faça um gráfico da saída y[n]=h[n] quando x[n]=δ[n].

c) Esboce w[n] para x[n]=2 δ[n]+4δ[n-4]-2δ[n-12].

Resolução :

5.a)

5.b)

5.c)

Prova 1 2020/2 - Sistemas de Controles Contínuos

1) Dado o circuito elétrico abaixo, assinale a alternativa que expressa corretamente a função de transferência G(s), onde:

Resposta:  Letra b)

2) Dado o diagrama  de fluxo de sinais abaixo, marque a alternativa correta  que representa a função de transferência do sistema, G(s).

Resposta: Letra a)

3) Dado o diagrama de blocos abaixo, assinale a alternativa que corresponde a simplificação do diagrama em um único bloco, ou seja, determinar função de transferência do sistema.

Resposta: Letra a)

4) Dada a função de transferência abaixo, assinale a opção correta para a saída do sistema para uma entrada degrau unitário:

Resposta: Letra b)

Sinais e Sistemas Lineares em tempo contínuo

4) A entrada de um sinal LIT estável e causal estão relacionados pela equação diferencial.

y' ' (t) + 7y ' (t) +12y ' (t) = x ' (t) + 4x (t)

a) Encontre H j( ω );

b) Encontre h (t) 

c) Encontre a resposta y(t) do sistema é x(t)= e^-t (t)

Resolução:

Prova 2 de Sinais: 2020/1

 2° avaliação de Sinais - Nota = 85%

1) Obtenha os coeficientes da série de Fourier em tempo discreto para o sinal x[n] dado abaixo. Desenvolver o problema passo a passo.

Resolução:

2) Para os sinais dados abaixo, obtenha a transformada de Fourrier de tempo discreto diretamente utilizando a definição. Assuma |y|<1. 

Resolução:

3) Considere um sistema LIT descrito pela equação de diferenças abaixo:

y[n]+ 7y[n -1] + 12y[n - 2] = x[n] + 2x[n - 1], determine:

4) Assinale com V(verdadeiro) ou com F(falso) as seguintes afirmações:

A sequência correta das afirmações dadas de cima para baixo, é:

a) (   ) V, V, V, F, F, V

b) (   ) V, F, F, V, F, F

c) (   ) F, F, V, F, F, V

d) (   ) F, F, F, V, F, V

e) (   ) F, V, V, F, F, V

Resolução:

Resposta letra: 

Lista 5 - Transformada Z

Resolução:

Lista 3: Transformada Z

Usando a definição de transformada Z, determine a transformada Z e a RDC para cada um dos seguintes sinais:

Resolução:

Lista 2: Série de Fourier Tempo Discreto

Dado o sinal abaixo, especificamos os coeficientes da série de Fourier de um sinal que é periódico com período 8. Determine o sinal x[n].

Resolução:

2) 

Resolução:

3)

Resolução: