Mecânica dos Fluidos "Exercicio 3"

1) A densidade de um líquido deve ser determinada por um velho hidrômetro cilíndrico com 1 cm de diâmetro cujas marcas de divisão foram completamente apagadas. A princípio o hidrometro é colocado na água e o nível de água é marcado. Em seguida, o hidrometro é solto no outro liquido e observa -se que a marca da água fica a 0,5 cm acima da interface entre o liquido e o ar. Se a altura da marca da água for 10 cm, determine a densidade do liquido.

2) Considere um grande bloco de gelo cúbico flutuando na água do mar. As densidades do gelo e da água do mar são 0,92 e 1,025, respectivamente. Se uma parte com 10 cm  de altura do bloco de gelo ficar acima da superfície da água, determine a altura do bloco abaixo da superfície.

F= Fb
ρ * g * Vt = ρf * g * Vsub
(Vsub / Vt) = ρcorpo / ρfluido
 hsub / ht = ρcorpo / ρfluido
h / h + 0,10 m = ρgelo / ρh2o
h / h + 0,10 m = 0,92 / 1,025

h= 0,876 m = 87,6 cm //

3) Um dos procedimentos comuns dos programas de condicionamento físico é determinar a relação entre gordura e músculo do corpo. Ela se baseia no principio de que o tecido muscular é mais denso do que o tecido gorduroso, portanto, quanto maior a densidade média do corpo, mais alta a fração de tecido muscular.  A densidade média do corpo pode ser determinada pesando -se a pessoa no ar e também enquanto ela está submersa na água de um tanque. Tratando todos os tecidos e ossos (além da gordura) como músculo com densidade equivalente a (p músculo) obtenha um relação para a fração de volume da gordura do corpo x gordo.

4) O volume e a densidade média de um corpo de forma irregular devem ser determinados usando -se uma balança de mola. O corpo pesa 7200 N no ar é 4,790 N na água. Determine o volume e a densidade do corpo.

RESOLUÇÃO:

m= 7200 N / 9,8
m= 734, 7 Kg

Fe= 7200 N - 4790 N
Fe= 2410 N

Fe= ρ*g * V
2410 N= 1000 Kg/ m³ * 9,8 * V
V= 0,246 m³

ρ= 734,7 Kg / 0,246 m³
ρ= 2986,58 Kg / m³
ρ= 3 X 10³ Kg / m³

d= 2986,58 / 1000
d= 2,99

4) Uma mangueira de jardim possui um diâmetro de 2 cm e está ligada a um irrigado que consiste num recipiente munido de 14 orificios, cada um dos quais com diametro de 0,14 cm. A velocidade da água na mangueira vale 0,85 m/s. Calcule a velocidade da água ao sair dos orifícios.

RESOLUÇÃO:

V1* A1= V2* A2
V2= (R² * V1) / n°

V2= (d) / n°² * d2²

V2= (0,02²)m  / (14* 1,4 X 10^-3)² m²
V2= 14,58 m/s

5) A água é bombeada continuamente de um porão inundado à velocidade de 5 m/s através de uma mangueira uniforme de raio de 1 cm. A mangueira passa através de uma janela que se encontra a 3 m acima do nível da água. Qual é a potência fornecida pela bomba ?

RESOLUÇÃO:
P= W / T

P= (m/t)* (g * h - 1/2 * V²)

ρ* A= 1000  * 3,14 X 10^-4 * 5 m/s
ρ= 1,57 Kg / s

P= ρ* A (g * h + 1/2 V²)

P= 1,57 * 9,8 * 3 + 1/2 * 5²
P= 58,65 W /

5) Um tanque de área muito grande está cheio de água até uma altura D= 30,5 cm o orifício de secção reta A= 6,45cm² , situado no fundo do tanque, permite drenar a água do interior.

a) Qual é a vazão na saída do orifício em cm³ / s ?

b) A que distancia abaixo do fundo do tanque a área da secção reta do jato se torna igual à metade da área do orifício ?

RESOLUÇÃO:

a)
V²= 2* g * h
V²= 2 * 9,8 * 0,305
V= 2,44 m/s

b)
p1 + p * g * d = p2 + 1/2 * p * V2²

D= (V3² - V2²) / 2* g

D= (4,8² - 2,44²) / 2* 9,8

D= 0,87 m //

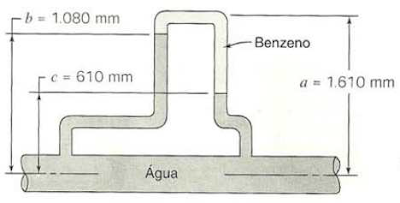
6) (Fox, Ex.13, pag. 55, 5ed.)A pressão num conduto de água e medida pelo manômetro de dois fluidos mostrados. Avalie a pressão manométrica no conduto.

7) (Fox, Ex.14, p´ag. 55, 5 ed.) Um manômetro e construído com tubo de vidro, com diâmetro interno uniforme D = 6,35 mm, conforme mostrado a seguir. O tubo em ∪ e preenchido parcialmente com água. Em seguida, um volume V = 3, 25 cm³ de óleo Meriam vermelho ´e adicionado no lado esquerdo, como se pode ver. Calcule a altura de equilíbrio, H, se ambas as pernas do tubo em ∪ estão abertas para a atmosfera.

8) (Fox, Ex.15, pag. 55, 5 ed.) O manômetro mostrado contem água e querosene. Com ambos os tubos abertos para atmosfera, as elevações da superfície livre diferem de H = 20 mm. Determine a diferença de elevação quando uma pressão de 98 Pa (manométrica) for aplicada no tubo.

9) (Fox, Ex.16, pag. 55, 5 ed.) O manômetro mostrado contem dois líquidos. O líquido. A tem densidade relativa igual a 0,88 e o líquido B tem densidade relativa igual a 2,95. Calcule a deflexão, h quando a diferença de pressão aplicada for p1 − p2 = 870 Pa.

10) Considere o manômetro de dois fluidos mostrados. Calcule a diferença de pressão aplicada.

11) Determine a pressão manométrica em psig no ponto a, se o líquido A tem densidade relativa igual a 0,75 e o líquido B tem densidade relativa igual a 1,20. O líquido em volta do ponto a e água e o tanque `a esquerda esta aberto para a atmosfera.

12) Considere um manômetro conectado como mostrado. Calcule a diferença de pressão.

13) A água flui para baixo ao longo de um tubo com inclinação de 30◦ com rela¸c˜ao `a horizontal, conforme mostrado. A diferença de pressão pA − pB e devida parcialmente a gravidade e parcialmente ao atrito. Obtenha uma expressão algébrica para a diferença de pressão. Calcule a diferença se L = 5 pes e h = 6 pol.