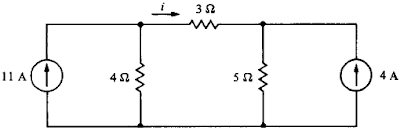
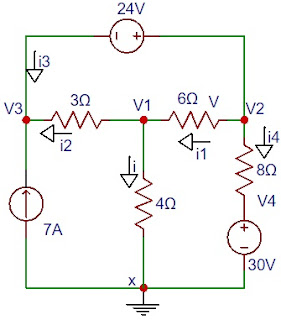
1)Usando a análise nodal, calcule V1, V2 e i no circuito abaixo. Resposta: V1=4V, V2=36V e i=4A.
Resolução
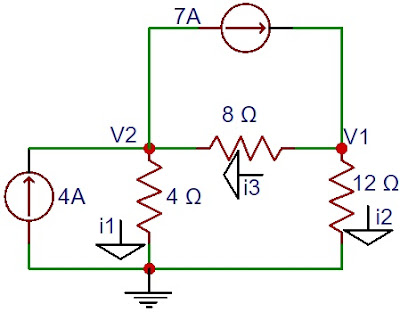 |
| Simulador EasyEDA |
LKC em V1
4 + i = 7 + i1
i - i1 = 3
OHM
1/8(V2 - V1) - 1/4(V1-0) = 3
V2 - V1 - 2V1 = 24
V2 - 3V1 = 24 (1)
LKC em V2
7 = i + i2
OHM
1/8(V2 - V1 + 1/12)(V2 - 0) = 7
(3V2 - 3V1 + 2V2)/24 = 7
5V2 - 3V1 = 168 (2)
(2) - (4)
5V2 - 3V1 = 168
-V2 + 3V1 = - 24
4V2 = 144
V2 = 36V
De (1)
36 - 3V1 = 24
V1= 4V
i = (36 - 4)/8 = 4A
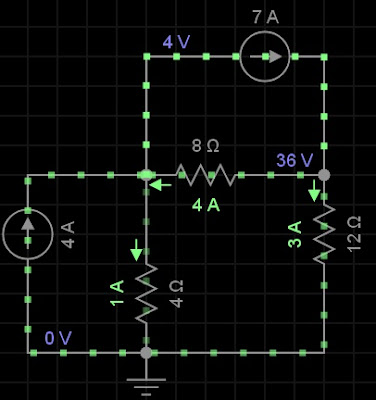 |
| Simulador EveryCircuit |
2) Repita o exercício anterior utilizando a análise de malha.
LKT em II
4(i2 - i1) + 8(i2 - i3) + 12i2 = 0
4(i2 - 4) + 8(i2 - i3) + 12i2 = 0
4i2 - 16 + 8i2 - 56 + 12i2 = 0
24i2 = 72
i2 = 3A
V1 = 4(i1 - i2) = 4(4-3) = 4V
V2 - V1 = 8(i3 - i2)
V2 - 4 = 8(7 - 3)
V2 = 36V
i = i3 - i2 = 7 - 3 = 1A
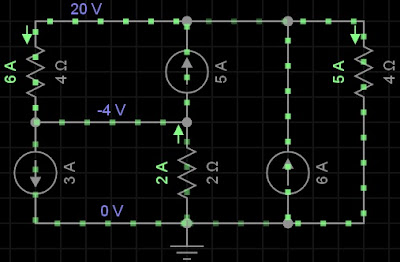
3) Usando a análise nodal, calcule V1, V2 e V3 no circuito abaixo. Resposta: V1= 24V, V2= - 4V e V3=20V.
Resolução
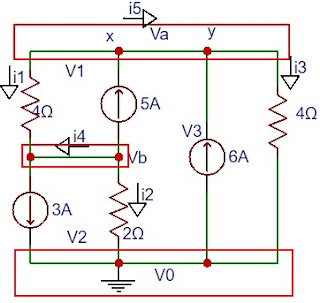 |
| Simulador EasyEDA |
LKC em Va
5 + 6 = i1 + i3
OHM
(Va - Vb ) /4
(Va - Vb) /4 + Va - 0)/4 = 11 (1)
LKC em Vb
i1 = 5 + i2 + 3
OHM
(Va - Vb) / 4 = Vb / 2 + 8 (2)
Va = 20V
Vb = - 4V
V1 = Va - Vb = 20 - (- 4) = 24V
V2 = Vb - 0 = - 4 = - 4V
Vb = Va - 0 = 20 V
 |
| Simulador EveryCircuit |
4) Repita o exercício anterior utilizando a análise de malha.
i2 - i3 = 5 (1)
i3 - i4 = 6 (2)
i1 = 3
LKT
2(i1 - i3) - 4i2 - 4i4 = 0
3 - i3 - 2i2 - 2i4 = 0
2i2 + 2i4 + i3 = 3 (3)
(1) + (2)
i2 - i4 = 11 (4)
(1) + (3)
3i2 + 2i4 = 8 (5)
2(4) + (5)
2i2 - 2i4 = 22
3i2 + 2i4 = 8
5i2 = 30
i2 = 6A
De (4)
6 - i4 = 11 => i4 = - 5A
De(2)
i3 - (-5) = 6 => i3 = 1A
V1 = 4i2 = 4 . 6 = 24V
V2 = 2(i3 - i1) = 2(1-3) = - 4V
LKT em i4
4i4 + V3 = 0
V3 = - 4i4 = - 4 . (-5) = 20V
5) Usando análise nodal, calcule v no circuito abaixo, se o elemento “desconhecido” é uma fonte independente de tensão de 4V com terminal positivo na parte superior. Resposta: v= 20V.
Resolução
 |
| Simulador EasyEDA |
LKC emV1
i2 = i3 + i
OHM
(V2 - V1) /6 = (V1 - V3) /3 + (V1 - 0)/4
(2V2 - 2V1) /12 = (4V1 - 4V3 + 3V1) /12
2V2 - 2V1 = 4V1 - 4V3 + 3V1
- 9V1 + 2V2 + 4V3 = 0 (1)
V2 - V3 = 24 (2)
V3 - 0 = 4
V3 = 4V
De (2)
V2 - 4 = 24 => V2 = 28V
D2 (1)
- 9V1 + 2 . 28 + 4 . 4 = 0
V1 = 8V
V = V2 - V1 = 28 - 8 = 20V
6) Repita o exercício anterior utilizando a análise de malha.
LKT em i2
4(i2 - i1) + 3(i2 - i1) + 3(i2 - i3) + 4 = 0 (1)
LKT em i1
-30 + 8i1 + 6(i1 - i3) + 4(i1 - i2) = 0 (2)
LKT em i3
3(i3 - i2) + 6(i3 - i1) + 24 = 0 (3)
i2 = -i (4)
Resolvendo; Logo:
i = 7/4A ; i1 = 1/4A ; i2 = - 7/4A ; i3 = - 37/12A
V = 6(i1 - i3) = 6[1/4 - (- 37/12) ] = 20V
7) Repita o exercício 5, se o elemento “desconhecido” é uma fonte independente de corrente de 7A
apontando para cima. Resposta: V = 26V.
Resolução:
 |
| Simulador EasyEDA |
Por análise de malha
LKT em i2
- 30 + 8i2 + 6(i2 - i3) + 4(i2 - i1) = 0 (1)
LKT em i3
3(i3 - i1) + 6(i3 - i2) + 24 = 0 (2)
Resolvendo, temos que:
i1 = - 7A
i2 = - 2A
i3 = -19/3 A
V = 6(i2 - i3) = 6[ - 2 - ( -19/3)] = 26V
8) Usando a análise de malhas, calcule i1 e i2 no circuito abaixo, se R1=2Ω, R2=4Ω, R3=3Ω, vg1=9V e vg2=-5V. Resposta: i1=3A, i2=2A.
LKC em i1
i1 . 2 + 3(i1 - i2) + i1 . 3 = 9
8i1 + i1.2 - 3i2 = 9
LKC em i2
4.i2 + 3(i2 - i1) = - 5
- 3.i1 + 7.i2 = -5
i1 = 3A
i2 = 2A
 |
| Simulador EveryCircuit |
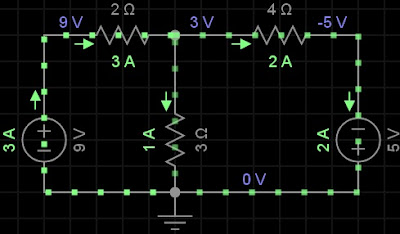
9) Repita o exercício anterior utilizando a análise nodal.
LKC em I3
I1 = I2 + I3
(V1 - V3)/2 = (V3 - V2)/4 + 3 - 0)/3 (1)
V1 - 0 = 9 = 9V
V2 - 0 = - 5 = - 5V
Logo; V3 = 3V
i1 = (V1 - V3)/2 = (9 - 3) / 2 = 3A
i2 = V3 - V2) / 4 = (3 - - 5) / 4 = 2A
I1 = I2 + I3
(V1 - V3)/2 = (V3 - V2)/4 + 3 - 0)/3 (1)
V1 - 0 = 9 = 9V
V2 - 0 = - 5 = - 5V
Logo; V3 = 3V
i1 = (V1 - V3)/2 = (9 - 3) / 2 = 3A
i2 = V3 - V2) / 4 = (3 - - 5) / 4 = 2A
10) Usando a análise de malhas, calcule i1 e i2 no circuito abaixo, se o elemento x é uma fonte de tensão independente de 6V, com terminal positivo na parte superior. Resposta: i1=2A, i2=1A.
Resolução:
LKT no sentido horário na malha 1
2i1 + 3(i1 - i2) = 16 - 9
5i1 - 3i2 = 7
6i2 + 3i2 - 3i1) = 9 - 6
-3i1 + 9i2 = 3
Resolvendo em álgebra
3.L1 + 5.L2
36.i2 = 36
i2 = 1A
5i1 - 3 . 1 = 7
i1 = 2A
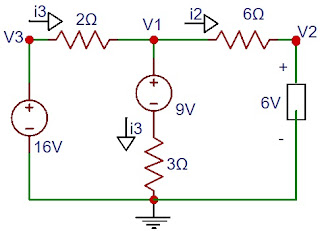
11) Repita o exercício anterior utilizando a análise nodal.
 |
| Simulador EasyEDA |
Resolução:
LKC em V1
i1 = i2 + i3 OHM (V3 - V1)/2 = (V1 - V2) /6 + i3 (1)
V1 - V4 = 9 (2)
V4 - 0 = 3i3 (3)
(2) + (3)
V1 = 9 + 3i3
i3 = (V1 - 9) / 3 (4)
(4) em (1)
(V3 - V1) /2 = (V1 - V2) /6 + (V1 - 9) /3 (5)
V3 - 0 = 16
V3 = 16V
V2 - 0 = 6 = 6V
De (5) temos;
V1 = 12V
i1 = (V3 - V1) /2 = (16 - 12 ) /2 = 2A
i2 = (12 - 6) / 6 = 1A
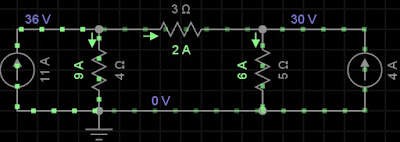
12) Usando a análise de malhas, calcule i1 no circuito abaixo. Resposta: i=2A .
Resolução:
LKT na malha 2
4(i2 - i1) + 3i2 + 5i(i2 - i3) = 0
- 4i1 + 12i2 - 5i3 = 0
i1 = 11A e i3 = 4A
- 4(11) + 12i2 - 5(4) = 0
i2= 2A
i2 = i = 2A
V= 3 . 2 = 6V
i = 6 / 3 = 2A
 |
| Simulador EveryCircuit |
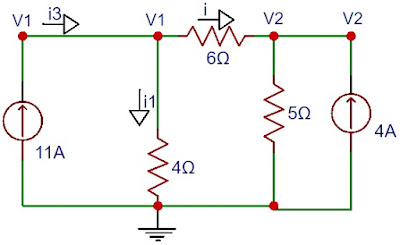
13) Repita o exercício anterior utilizando a análise nodal.
Resolução
 |
| Simulador EasyEDA |
LKC em V1
11 = i + i1 OHM (V1 - V2) /3 + (V1 - 0)/4 = 11 (1)
LKC em V2
i + 4 = i2 OHM (V1 - V2) /3 + 4 = (V2 - 0) /5 (2)
V1 = 35V
V2 = 30V
i = (V1 - V2) /3 = (36 - 30) /3 = 2A
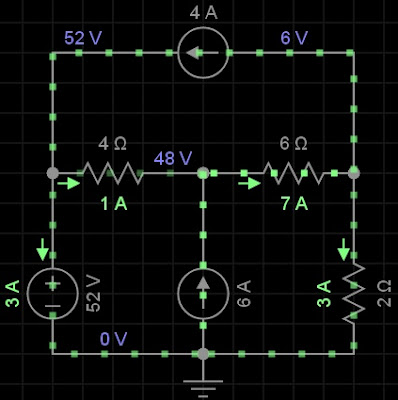
14) No circuito abaixo, considere R1= 4Ω, R2 = 6Ω, R3 = 2Ω, ig1 = 4A,e ig2 = 6A e vg3 = 52V. Mantendo i2 e i3 como indicado e trocando i1 para uma corrente de laço no sentido horário que passa através de R1, R2 e R3 e vg3, empregue a análise de malha para encontrar a potência entregue a R3 (note que neste caso a corrente em e R3 é i1 + i3). Resposta: 18W.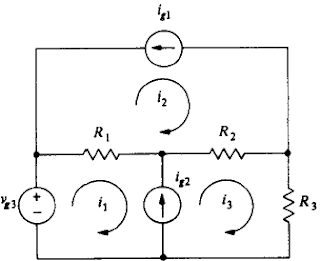

i2 = - 4A e i3 = 6A
LKT em ABCD
4(i1 - i2) + 6(i1 + i3 - i2) + 2(i1 + i3) - 52 = 0
12i1 - 10i2 + 8i3 = 52
12i1 = - 36
i1 = -3A
P = R . i . i = 2(-3 . -3) = 18W
 |
| Simulador EveryCircuit |
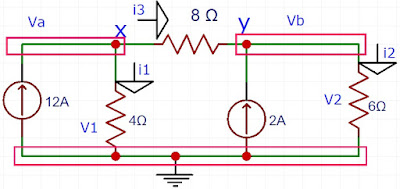
15) Usando a análise nodal, calcule V1 e V2 no circuito abaixo. Resposta: V1=40V, V2=24V.
 |
| Simulador EasyEDA |
LKC em x 12 = i1 + i3 OHM (Va - 0)/4 + Va - Vb) /8 = 12 (1)
LKC em y i3 + 2 = i2 OHM (Va - Vb) /8 + 2 = (Vb - 0) /6 (2)
Va = 40V V1 = Va - 0 = 40 = 40V
Vb = 24V V2 = Vb - 0 = 24 = 24V
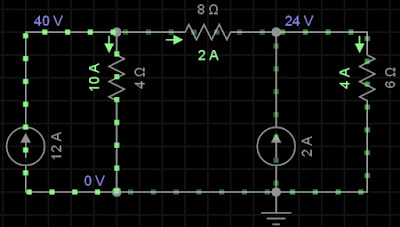 |
| Simulador EveryCircuit |
16) Repita o exercício anterior utilizando a análise de malha.
i1 = 12A
i3 - i2 = 2 (1)
LKT em ABCD
4(i2 - i1) + 8i2 + 6i3 = 0
- 4i1 + 12i2 + 6i3 = 0
i1 = 12A
i2 = 2A
i3 = 4A
V1 = 4(i1 - i2) = 4(12 - 2) = 40V
V2 = 6i3 = 6 . 4 = 24V
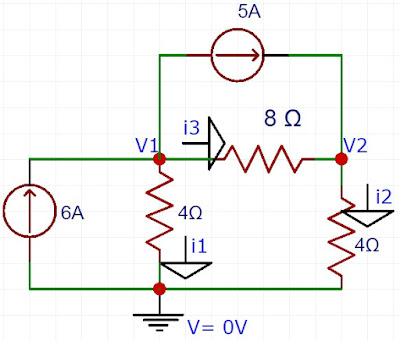
17) Usando a análise nodal, calcule i1 e i2 no circuito abaixo. Resposta: i1= 2A, i2= 4A.
 |
| Simulador EasyEDA |
LKC em V1 6 = i1 + i3 + 5
i1 + i3 = 1 OHM V1 /4 + (V1 - V2) /8 = 1
LKC em V2
i3 + 5 = i2
OHM (V1 - V2) /8 + 5 = V2 /4
V1 = 8V
V2 = 16V
i1 = V1 / 4 = 8/4 = 2A
i2 = V2 /4 = 16/4 = 4A
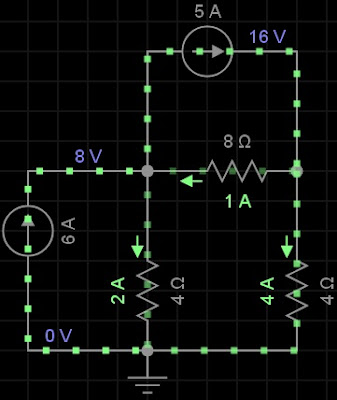 |
| Simulador EveryCircuit |
18) Repita o exercício anterior utilizando a análise de malha.
i3 = 6A
i4 = i2 (1)
i5 = 5A
LKT em i4
4(i4 - i3) + 8(i4 - i5) + 4i4 = 0 (2)
(1) em (2)
i1 = i3 - i4 = 6 - 4 = 2A
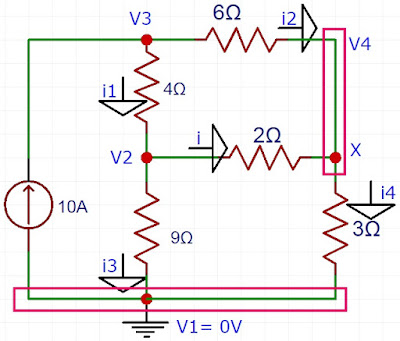
19) Usando a análise nodal, calcule i no circuito abaixo. Resposta: i=3A.
 |
| Simulador EasyEDA |
LKC em V3
10 = i1 + i2 OHM (V3 - V2) /3 + (V3 - V4) /6 = 10
LKC em V2
i1 = i + i3 OHM (V3 - V2) /3 = (V2 - V4) /2 + V2/4
LKC em X
i + i2 = i4 OHM (V2 - V4) /2 + (V3 - V4) /6 = V4 /3
V2 = 27V
V3 = 45V
V4 = 24V
i = (27 - 21) /2 = 3A
 |
| simulador EveryCircuit |
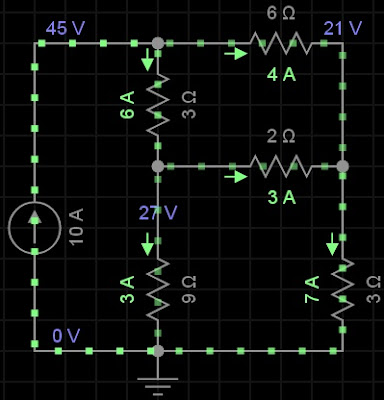
20) Repita o exercício anterior utilizando a análise de malha.
i1 = 10A
LKT em i2
3(i2 - i1) + 6i2 + 2(i2 - i3) = 0
LKT em i3
9(i3 - i1) + 2(i3 - i2) + 3i3 = 0
i2 = 4A
i3 = 7A
i = 7 - 4 = 3A
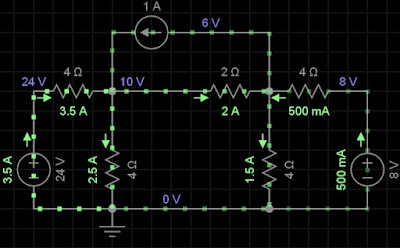
21) Usando a análise nodal, calcule i no circuito abaixo. Resposta: i=2A.
LKC em V1
1 = i1 + i + i2 OHM (V1 - V3) /4 + (V1 - V2) /2 + V1 /4 = 1
LKC em V2
i = 1 + i3 + i4 OHM (V1 - V2) /2 = 1
(V1 - V2) /2 = 1 + 2 - 0) /4 + (V2 - V4) /4
V4 - 0 = 8 = 8V
V3 - 0 = 24 = 24V
V1 = 10V
V2 = 6V
V3 = 24V
V4 = 8V
i = (V1 - V2) /2 = (10 - 6) /2 = 2A
 |
| simulador EveryCircuit |
i2 = -1A
LKT em i1
4i1 + 4(i1 - i3) = 24
8i1 - 4i3 = 24
LKT em i3
4(i3 - i1) + 2(i3 - i2) + 4(i3 - i4) = 0
- 4i1 - 2i2 + 10i3 - 4i4 = 0
LKT em i4
4(i4 - i3) + 4i4 = - 8
- 4i3 + 8i4 = -8
Resolvendo por algebra
i1 = 7A
i3 = 1A
i4 = - 1/2
i = i3 - i2 = 1 - (-1) = 2A
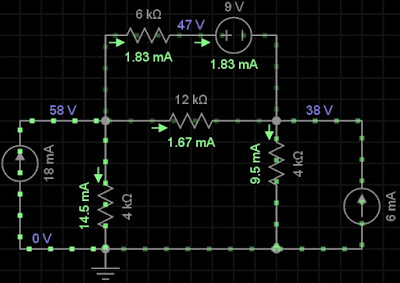
23) Usando a análise nodal, calcule v no circuito abaixo. Resposta: v= 20V.
LKC em A
18x10-3 = i1 + i2 + i3 OHM (V2 - 0) /4x103 + V2 - V3) /12x103 + (V2 - V1) /6103 = 18x 10-3
LKC em B i3 + i2 + 6x10-3 = i4
OHM (V2 - V4) /6x103 + (V2 - V3) /12x103 + 6x103 = ((V3 - 0) /4x103
V4 - V3 = 9
V2 = 58V
V4 = 47V
V = V2 - V3 = 58 - 38 = 20V
 |
| Simulador EveryCircuit |
24) Repita o exercício anterior utilizando a análise de malha.
i1 = 18x10-3 A
i4 = - 6x10-3
LKT em i2
[6i2 + 12(i2 - i3)]103 = -12
LKT em i3
[ 4(i3 - i3) + 12(i3 - i2) + 4(i3 - i4) ]103 = 0
i1 = 9 / 500 = 0,018A
Va - 0 = 4(i1 - i3)103 = 4(9/500 - 7/2000)103 = 58V
i2 = 11/600 A
i3 = 7 / 200 A
Vb - 0 = 4(i3 - i4)103= 4[7/200 - ( -3/500) ] 103
i4 = -3/500A
Vb = 38V
V = Va - Vb = 58 - 38 = 20V
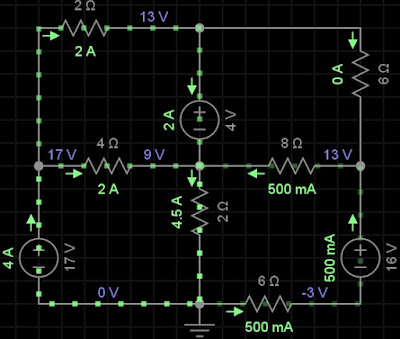
25) Resolva o circuito abaixo, se as fontes de corrente de 2A, 3A e 7A são substituídas por fontes de tensão de, respectivamente, 17V, 4V e 16V, sendo o terminal positivo a parte superior de cada uma delas.
2i1 + 4(i1 - i2) = - 4
6i1 - 4i2 = - 4
4(i2 - i1) + 2(i2 - i4) = 17
- 4i1 + 6i2 - 2i4 = 17
6i3 + 8(i3 - i4) = 4
14i3 - 8i4 = 4
8(i4 - i3) + 2(i4 - i2) + 6i4 = - 16
- 2i2 - 8i3 + 16i4 = -16
Resolvendo por algebra
i1 = 2A i2 = 4A
i3 = 0A i4 = - 1/2A
V = 4(i2 - i1) = 4(4 - 2) = 8V
 |
| Simulador EveryCircuit |
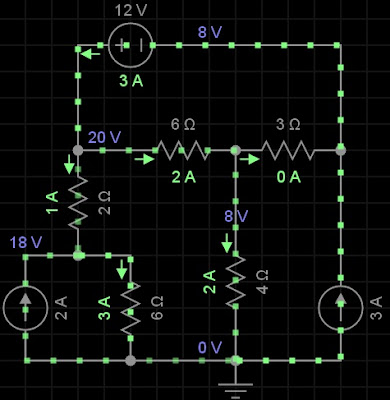
26) Calcule v usando o método (nodal ou de malhas) que requer o menor número de equações.
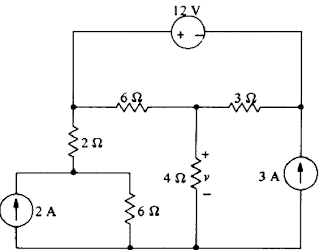
Por analise de Malha
i1 = 2A
i4 = - 3A
LKT em i2
6(i2 - i1) + 2i2 + 6(i2 - i3) + 4(i2 - i4) = 0
- 12i1 + 18i2 - 6i3 - 4i4 = 0
LKT em i3
3(i3 - i4) + 6(i3 - i2) = - 12
- 6i2 + 9i3 - 3i4 = -12
Algebra
i1 = 2A
i2 = - 1A
i3 = - 3A
i4 = - 3A
V = 4(i2 - i4) = 4(-1 + 3) = 8V
 |
| Simulador EveryCircuit |