Pesquisar neste blog
26/01/2019
Matriz com números aleatórios em Java
/*Faça um algoritmo de uma matriz 4x4 com valores aleatórios entre 0 e 100. Apos isso determine o maior número da matriz e a sua posição.*/
import java.util.Random;
public class Main{
public static void main(String[] args){
int[][] numAleatorio = new int [4][4];
Random numeroRandom = new Random();
for (int i = 0; i < numAleatorio.length; i++){
for (int j = 0; j < numAleatorio[i].length; j++){
numAleatorio[i][j] = numeroRandom.nextInt(100);//gera numero aleatorio de 0 a 100
}
}
//int maior = Integer.MIN_VALUE;
int maior = 0, linha = 0, col = 0;
for (int i = 0; i < numAleatorio.length; i++){
for (int j = 0; j < numAleatorio[i].length; j++){
if(numAleatorio[i][j] > maior){
maior = numAleatorio[i][j];
linha = i;
col = j;
}
}
}
System.out.print("\t\tMatriz\n");
for (int i = 0; i < numAleatorio.length; i++){
for (int j = 0; j < numAleatorio[i].length; j++){
System.out.print("\t"+numAleatorio[i][j]+" ");
}
System.out.println();
}
System.out.println("\nMaior valor = "+maior);
System.out.println("Linha: "+linha);
System.out.println("Coluna:"+col);
}
}
20/01/2019
Desenhando um smille em java
Classe DesenhoComponente
import java.awt.Color;
import java.awt.Graphics;
import javax.swing.JPanel;
public class DesenhoComponente extends JPanel{
public void paintComponent( Graphics g ){
super.paintComponent(g);
// desenhar o rosto
g.setColor( Color.YELLOW );
g.fillOval( 10, 10, 200, 200 );
// desenhar os olhos
g.setColor( Color.BLACK );
g.fillOval( 55, 65, 30, 30 );
g.fillOval( 135, 65, 30, 30 );
// desenhar a boca
g.fillOval( 50, 110, 120, 60 );
// "retocar" a boca em um sorriso
g.setColor( Color.YELLOW );
g.fillRect( 50, 110, 120, 30 );
g.fillOval( 50, 120, 120, 40 );
}
}
__________ / / ________
Código fonte principal
import javax.swing.JFrame;
public class DrawSmiley
{
public static void main( String[] args )
{
DesenhoComponente painel = new DesenhoComponente();
JFrame aplicacao = new JFrame();
aplicacao.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE );
aplicacao.add( painel );
aplicacao.setSize( 230, 250 );
aplicacao.setVisible( true );
}
}
Palavras chave:
Drawing a smille in java
Dibujo de un smille en java
Teken 'n glimlag in java
رسم smille في جافا
জাভা একটি স্মাইল অঙ্কন
Pagguhit ng isang smille sa java
Teikna broskalla í Java
Smink rajzolása a java-ban
Ngirim smile ing jawa
Parando Smille in Java
Parando Smille in Java
import java.awt.Color;
import java.awt.Graphics;
import javax.swing.JPanel;
public class DesenhoComponente extends JPanel{
public void paintComponent( Graphics g ){
super.paintComponent(g);
// desenhar o rosto
g.setColor( Color.YELLOW );
g.fillOval( 10, 10, 200, 200 );
// desenhar os olhos
g.setColor( Color.BLACK );
g.fillOval( 55, 65, 30, 30 );
g.fillOval( 135, 65, 30, 30 );
// desenhar a boca
g.fillOval( 50, 110, 120, 60 );
// "retocar" a boca em um sorriso
g.setColor( Color.YELLOW );
g.fillRect( 50, 110, 120, 30 );
g.fillOval( 50, 120, 120, 40 );
}
}
__________ / / ________
Código fonte principal
import javax.swing.JFrame;
public class DrawSmiley
{
public static void main( String[] args )
{
DesenhoComponente painel = new DesenhoComponente();
JFrame aplicacao = new JFrame();
aplicacao.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE );
aplicacao.add( painel );
aplicacao.setSize( 230, 250 );
aplicacao.setVisible( true );
}
}
 |
| Impressão do smille |
Palavras chave:
Drawing a smille in java
Dibujo de un smille en java
Teken 'n glimlag in java
رسم smille في جافا
জাভা একটি স্মাইল অঙ্কন
Pagguhit ng isang smille sa java
Teikna broskalla í Java
Smink rajzolása a java-ban
Ngirim smile ing jawa
Parando Smille in Java
Parando Smille in Java
13/01/2019
Sequencial de 10 LEDs
Sequência de 10 LEDs com ci 555 + 7490 + 7442, ideal para luminárias de natal
Componentes utilizados:
1 ci 555
1 ci 7490
1 ci 74HC42
1 Potenciômetro 150KΩ
11 Resistores 150Ω a 390Ω
11 Leds
1 Capacitor 10uF
1 Resistor 10KΩ
1 Resistor de 1KΩ
Clique aqui para fazer o download do arquivo feito no Proteus 8
Créditos para: http://www.ezuim.com/pdf/seq_10leds.pdf
Palavras chave:
Последовательность из 10 светодиодов ci 555 + 7490 + 7442
Seicheamh 10 stiúir le 555 + 7490 + 7442
Sequence 10 LED með ci 555 + 7490 + 7442
Volgorde van 10 LED's met ci 555 + 7490 + 7442
Пасля 10 святлодыёдаў з Х 555 + 7490 + 7442
ci 555 + 7490 + 7442の10個のLEDのシーケンス
ci 555 + 7490 + 7442가있는 10 개의 LED 시퀀스
Secuencia de 10 LEDs con ci 555 + 7490 + 7442
Ci 555 + 7490 + 7442 ile 10 LED dizisi
Sekwencja 10 diod LED z ci 555 + 7490 + 7442
Componentes utilizados:
1 ci 555
1 ci 7490
1 ci 74HC42
1 Potenciômetro 150KΩ
11 Resistores 150Ω a 390Ω
11 Leds
1 Capacitor 10uF
1 Resistor 10KΩ
1 Resistor de 1KΩ
 |
| Sequênciador de leds com ci 555, 7490 e 74HC42 |
Clique aqui para fazer o download do arquivo feito no Proteus 8
Créditos para: http://www.ezuim.com/pdf/seq_10leds.pdf
Palavras chave:
Последовательность из 10 светодиодов ci 555 + 7490 + 7442
Seicheamh 10 stiúir le 555 + 7490 + 7442
Sequence 10 LED með ci 555 + 7490 + 7442
Volgorde van 10 LED's met ci 555 + 7490 + 7442
Пасля 10 святлодыёдаў з Х 555 + 7490 + 7442
ci 555 + 7490 + 7442の10個のLEDのシーケンス
ci 555 + 7490 + 7442가있는 10 개의 LED 시퀀스
Secuencia de 10 LEDs con ci 555 + 7490 + 7442
Ci 555 + 7490 + 7442 ile 10 LED dizisi
Sekwencja 10 diod LED z ci 555 + 7490 + 7442
12/01/2019
Semáforo com CI 4017 + 555
Componentes utilizados:
1 ci 555
1 ci 4017
2 leds vermelhos
2 leds amarelos
2 leds verdes
1 led qualquer
15 diodos 1N4148
1 capacitor 10 uF
1 resistor de 47KΩ
1 resistor de 1KΩ
1 resistor de 220Ω
Clique aqui para fazer o download do arquivo feito no Proteus 8
Créditos para: http://circuitdesolator.blogspot.com/2011/01/traffic-light-circuit-based-on-4017.html
Palavras chave:
Semaphore with CI 4017 + 555
Semaphore oo leh CI 4017 + 555
Semaphore met CI 4017 +555
Semaphor mit CI 4017 + 555
Semaphore հետ CI 4017 + 555
Святло з CI 4017 + 555
Semaphore ndi CI 4017 + 555
CI 4017 + 555 සමඟ Semaphore සමඟ
Semaphore ak CI 4017 + 555
Semaphore s CI 4017 + 555
Semafor CI 4017 + 555-ga
Sémaphore avec CI 4017 + 555
סעמאַפאָרע מיט סי 4017 +555
Seapaphar le CI 4017 + 555
Семафор с CI 4017 + 555
 |
| Semáforo com ci 4017 e 555 |
Clique aqui para fazer o download do arquivo feito no Proteus 8
Créditos para: http://circuitdesolator.blogspot.com/2011/01/traffic-light-circuit-based-on-4017.html
Palavras chave:
Semaphore with CI 4017 + 555
Semaphore oo leh CI 4017 + 555
Semaphore met CI 4017 +555
Semaphor mit CI 4017 + 555
Semaphore հետ CI 4017 + 555
Святло з CI 4017 + 555
Semaphore ndi CI 4017 + 555
CI 4017 + 555 සමඟ Semaphore සමඟ
Semaphore ak CI 4017 + 555
Semaphore s CI 4017 + 555
Semafor CI 4017 + 555-ga
Sémaphore avec CI 4017 + 555
סעמאַפאָרע מיט סי 4017 +555
Seapaphar le CI 4017 + 555
Семафор с CI 4017 + 555
11/01/2019
CI 74LS95
Registrador de deslocamento com CI 74LS95
Clique aqui para fazer o download do arquivo feito no Proteus 8.6
Palavras chave:
Ofsetový registr s CI 74LS95
CI 74LS95 ഉപയോഗിച്ച് ഓഫർ രജിസ്റ്റർ ചെയ്യുക
使用CI 74LS95進行偏移寄存器
تسجيل الأوفست مع CI 74LS95
Offsetregister mit CI 74LS95
Yambani kulembetsa ndi CI 74LS95
Offset register med CI 74LS95
Offset register CI 74LS95-ga
Afrekeningsregister met CI 74LS95
Registrasi offset dengan CI 74LS95
CI 74LS95 бүхий офсет бүртгэл
Diiwaangelinta furfurista ee CI 74LS95
 |
| Simulador Proteus 8.6 |
Clique aqui para fazer o download do arquivo feito no Proteus 8.6
Palavras chave:
Ofsetový registr s CI 74LS95
CI 74LS95 ഉപയോഗിച്ച് ഓഫർ രജിസ്റ്റർ ചെയ്യുക
使用CI 74LS95進行偏移寄存器
تسجيل الأوفست مع CI 74LS95
Offsetregister mit CI 74LS95
Yambani kulembetsa ndi CI 74LS95
Offset register med CI 74LS95
Offset register CI 74LS95-ga
Afrekeningsregister met CI 74LS95
Registrasi offset dengan CI 74LS95
CI 74LS95 бүхий офсет бүртгэл
Diiwaangelinta furfurista ee CI 74LS95
09/01/2019
Contador de 0 a 59
Contador com CI 74LS90 , 555 e 74LS47
Clique aqui para fazer o download do arquivo feito no Proteus 8.6
Palavras chave:
Räknare från 0 till 59
Ka soo horjeedka 0 ilaa 59
0에서 59 사이의 카운터
Лічыльнік ад 0 да 59
計數器從0到59
Μετρητής από 0 έως 59
Penghitung dari 0 hingga 59
Contatore da 0 a 59
0 മുതൽ 59 വരെ
0 ile 59 arasındaki sayaç
Počítadlo od 0 do 59
 |
| Simulador Proteus 8.6 |
Clique aqui para fazer o download do arquivo feito no Proteus 8.6
Palavras chave:
Räknare från 0 till 59
Ka soo horjeedka 0 ilaa 59
0에서 59 사이의 카운터
Лічыльнік ад 0 да 59
計數器從0到59
Μετρητής από 0 έως 59
Penghitung dari 0 hingga 59
Contatore da 0 a 59
0 മുതൽ 59 വരെ
0 ile 59 arasındaki sayaç
Počítadlo od 0 do 59
04/01/2019
Contador crescente / decrescente
Contador crescente e decrescente mestre escravo no Logisim usando túnel
Clique aqui para fazer o download do arquivo feito no Logsisim
Palavras chave:
Count increasing and decreasing master slave in Logisim using tunnel
Contador creciente y decreciente maestro esclavo en el Logisim usando túnel
Tel die toenemende en afnemende meesterslaaf in Logisim deur tonnel te gebruik
ዋሻ (ዋሻ) በመጠቀም ሎይስስሚን ሎይስምን በመጨመር እና በመቀነስ ላይ
العد زيادة وانخفاض الرقيق الرئيسي في Logisim باستخدام النفق
да лічыльніка і памяншэння гаспадара рабоў пры выкарыстанні Logisim тунэля
Избройте увеличаването и намаляването на главния slave в Logisim, използвайки тунел
Pagdugang sa pagdugang ug pagkunhod sa master slave sa Logisim gamit ang tunnel
使用隧道計算Logisim中增加和減少主從屬的數量
터널을 사용하여 Logisim에서 마스터 슬레이브 수를 늘리고 줄입니다.
Konte ogmante ak diminye mèt esklav nan Logisim lè l sèvi avèk tinèl
Tæl stigende og faldende master slave i Logisim ved hjælp af tunnel
Compter les esclaves maîtres croissants et décroissants dans Logisim à l'aide d'un tunnel
Steigerje en ferheegjen master slave yn Logisim mei tunnel
Hitung peningkatan dan penurunan master slave di Logisim menggunakan terowongan
Conta aumentando e diminuendo lo slave master in Logisim usando tunnel
Telling økende og avtagende mester slave i Logisim ved hjelp av tunnel
Tirada addoonta oo kordhaya oo yareynaya Logisim iyadoo la adeegsanayo tunnel
Räkna ökande och minskar mästarslav i Logisim med tunnel
 |
| Simulador Logisim |
Clique aqui para fazer o download do arquivo feito no Logsisim
Palavras chave:
Count increasing and decreasing master slave in Logisim using tunnel
Contador creciente y decreciente maestro esclavo en el Logisim usando túnel
Tel die toenemende en afnemende meesterslaaf in Logisim deur tonnel te gebruik
ዋሻ (ዋሻ) በመጠቀም ሎይስስሚን ሎይስምን በመጨመር እና በመቀነስ ላይ
العد زيادة وانخفاض الرقيق الرئيسي في Logisim باستخدام النفق
да лічыльніка і памяншэння гаспадара рабоў пры выкарыстанні Logisim тунэля
Избройте увеличаването и намаляването на главния slave в Logisim, използвайки тунел
Pagdugang sa pagdugang ug pagkunhod sa master slave sa Logisim gamit ang tunnel
使用隧道計算Logisim中增加和減少主從屬的數量
터널을 사용하여 Logisim에서 마스터 슬레이브 수를 늘리고 줄입니다.
Konte ogmante ak diminye mèt esklav nan Logisim lè l sèvi avèk tinèl
Tæl stigende og faldende master slave i Logisim ved hjælp af tunnel
Compter les esclaves maîtres croissants et décroissants dans Logisim à l'aide d'un tunnel
Steigerje en ferheegjen master slave yn Logisim mei tunnel
Hitung peningkatan dan penurunan master slave di Logisim menggunakan terowongan
Conta aumentando e diminuendo lo slave master in Logisim usando tunnel
Telling økende og avtagende mester slave i Logisim ved hjelp av tunnel
Tirada addoonta oo kordhaya oo yareynaya Logisim iyadoo la adeegsanayo tunnel
Räkna ökande och minskar mästarslav i Logisim med tunnel
30/12/2018
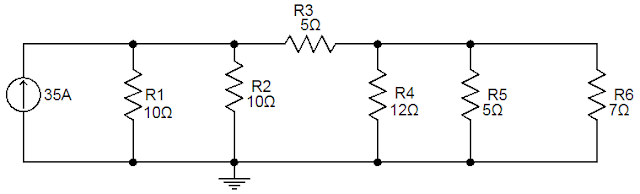
DIVISOR DE CORRENTE
Exercícios resolvidos com divisor de corrente
Resolução
iR1= iR2 = 45/10 = 4,5 A
iR3 = 45/15 = 3A
iR4 = 45/12 = 3,75A
iR5 = 45/5 = 9A
iR6 = 45/7 = 6,43A
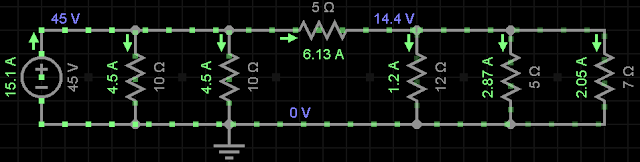
Resolução:
Req = 2,9751 = 2,98Ω
iR1 = iR2 = 45/10 = 4,5A
i = V / Req = 45 / 2,98 = 15,1 A
i1 = i - iR1 = 15,1 - 4,5 = 10,6 A
i2 = i1 - iR2 = 10,6 - 4,5 = 6,13 A
LKT
10 . 4,5 - 6,13 . 5 - VR4 = 0
VR4 = 14,4V
iR4 = 14,4 / 12 = 1,2A
iR5 = 14,4 / 5 = 2,87A
iR6 = 14,4 / 7 = 2,05A
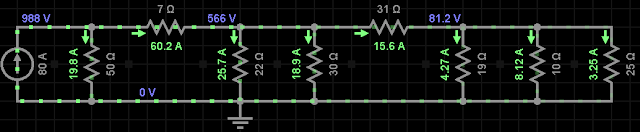
Resolução:
Req = 12,35Ω
V = 12,35 . 80 = 988V
iR1 = 998 / 50 = 19,8 A
iR3 = i - iR1 = 80 - 19,8 = 60,2 A
LKT 19,76 . 50 - 60,24 . 7 - V = 0
V = 566 V
iR2 = 566 / 22 = 25,7 A
iR4 = 566 / 30 = 18,86 = 18,9 A
V = 81,2 V
iR6 = 81,2 / 19 = 4,27A
iR7 = 81,2 / 10 = 8,12A
iR8 = 81,2 / 25 = 3,25A
Resolução:
Req = 13,4Ω
i = 50 / 13,4 = 3,73 A
iR1 = 50/ 55= 909 mA
iR3 = 3,73 - 0,909 = 2,82 A
VR3 = 2,82 . 12 = 33,84V
LKT
VR2 = - 33,84 + 0,909 . 55 = 16,1V
iR2 = 16,1 / 10 = 1,61A
iR5 = 3,73 - 0,909 -2,82 -0,733 -1,61 = 0,475 = 475A
LKT
10 . 1,61 - 31 . 0,475 - VR6 = 0
VR6 = 1,4 V
iR7 = 1,4 / 10 = 140 mA
iR8 = 1,4 / 5 = 280 mA
Ex6)
Resolução:
iR1 = iR2 = iR... 200 / 550 = 0,364 A = 364 mA
Ex7)
Resolução:
iR1 = 40 / 12 = 3,3333... A
iR2 = 0 A
iR3 = 40 / 25 = 1,6 A
Ex8)
Resolução:
Divisor de corrente
Corrente procurada
i = (Corrente da fonte x corrente no resistor que eu não quero) / (resistor que não quero + resistor que eu quero)
iR2 = ( -50 . 25) / (25 + 12) = - 33,78 = - 33,8 A
iR1 = (- 50 . 12) / (12 + 25) = - 16,22 A
Ex9)
Resolução:
Divisor de corrente para fonte de 12V
iR2 = 12 / 15 = 0,8A
iR4 = 12 / 19 = 0,631A
Para fonte de 50A com resistor de 25Ω e 12Ω o método por divisor de corrente já não se aplica, o mais adequado seria usar o método da análise de malhas ou um outro qualquer.
Ex10)
Resolução:
Req = 4,12Ω
i = V / Req V = i . Req = 50 . 4,12 = 206V
iR1 = 206 / 30 = 6,87A
iR2 = 206 / 15 = 13,7A
iR3 = 206 / 25 = 8,24A
iR4 = 206 / 19 = 10,8A
iR5 = 206 / 20 = 10,3A
Ex11)
Resolução:
Req = 16 + (6 . 12 / (6+12)) = 20Ω
Divisor de corrente
Corrente procurada
Corrente i = (fonte corrente x res que eu não quero) / (res que eu não quero + res que eu quero)
iR1 = 30. 20 / (20+5) = 24A
iR2 = 30 . 5 / (5+20) = 6A
iR3 = 6 . 12 / (6+12) = 2A
iR = 6 . 6 / (12+6) = 4A
Obs: No resistor de 6Ω e 12Ω só possível aplicar o divisor de corrente se for um fonte isolada com apenas uma fonte corrente ou tensão, caso contrário é preciso usar outro método.
Palavras chave:
Vermogensverdeler
Kragverdeler
Leistungsteiler
مقسم الطاقة
Power divider
бягучы Дзельнік
Разделител на мощността
Wopatula mphamvu
功率分配器
Razdjelnik snage
מחלק כוח
Vermogensverdeler
Power divider
Güç bölücü
Ex1)
Resolução
iR1= iR2 = 45/10 = 4,5 A
iR3 = 45/15 = 3A
iR4 = 45/12 = 3,75A
iR5 = 45/5 = 9A
iR6 = 45/7 = 6,43A
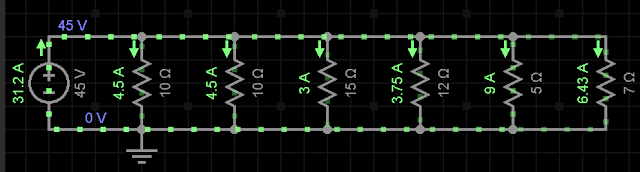 |
| Simulador EveryCircuit |
Ex2)
Resolução:
Req = 2,9751 = 2,98Ω
iR1 = iR2 = 45/10 = 4,5A
i = V / Req = 45 / 2,98 = 15,1 A
i1 = i - iR1 = 15,1 - 4,5 = 10,6 A
i2 = i1 - iR2 = 10,6 - 4,5 = 6,13 A
LKT
10 . 4,5 - 6,13 . 5 - VR4 = 0
VR4 = 14,4V
iR4 = 14,4 / 12 = 1,2A
iR5 = 14,4 / 5 = 2,87A
iR6 = 14,4 / 7 = 2,05A
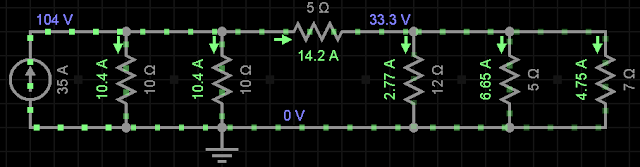
Req = 2,9751Ω
i = V / Req V= i . Req
V = 35 . 2,9751 = 104,12 V
iR1 = iR2 = 104,12 / 10 = 10,4 A
iR3 = 35 - 10,4 - 10,4 = 14,2A
VR4 = -14,2 . 5 + 10 . 10,4 = 33,3 V
iR4 = 33,3 / 12 = 2,77 A
iR5 = 33,3 / 5 = 6,65 A
iR6 = 33,3 / 7 = 4,75 A
i = V / Req V= i . Req
V = 35 . 2,9751 = 104,12 V
iR1 = iR2 = 104,12 / 10 = 10,4 A
iR3 = 35 - 10,4 - 10,4 = 14,2A
VR4 = -14,2 . 5 + 10 . 10,4 = 33,3 V
iR4 = 33,3 / 12 = 2,77 A
iR5 = 33,3 / 5 = 6,65 A
iR6 = 33,3 / 7 = 4,75 A
Ex4)
Resolução:
Req = 12,35Ω
V = 12,35 . 80 = 988V
iR1 = 998 / 50 = 19,8 A
iR3 = i - iR1 = 80 - 19,8 = 60,2 A
LKT 19,76 . 50 - 60,24 . 7 - V = 0
V = 566 V
iR2 = 566 / 22 = 25,7 A
iR4 = 566 / 30 = 18,86 = 18,9 A
V = 81,2 V
iR6 = 81,2 / 19 = 4,27A
iR7 = 81,2 / 10 = 8,12A
iR8 = 81,2 / 25 = 3,25A
Ex5)
Resolução:
Req = 13,4Ω
i = 50 / 13,4 = 3,73 A
iR1 = 50/ 55= 909 mA
iR3 = 3,73 - 0,909 = 2,82 A
VR3 = 2,82 . 12 = 33,84V
LKT
VR2 = - 33,84 + 0,909 . 55 = 16,1V
iR2 = 16,1 / 10 = 1,61A
iR5 = 3,73 - 0,909 -2,82 -0,733 -1,61 = 0,475 = 475A
LKT
10 . 1,61 - 31 . 0,475 - VR6 = 0
VR6 = 1,4 V
iR7 = 1,4 / 10 = 140 mA
iR8 = 1,4 / 5 = 280 mA
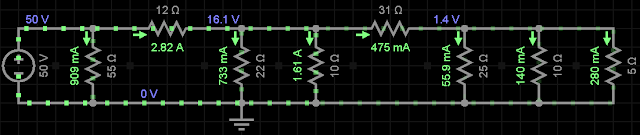 |
| Simulador EveryCircuit |
Ex6)
Resolução:
iR1 = iR2 = iR... 200 / 550 = 0,364 A = 364 mA
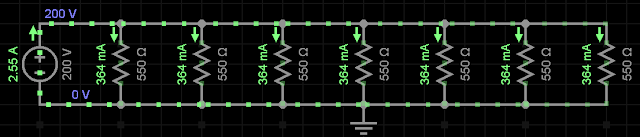 |
| Simulador EveryCircuit |
Ex7)
Resolução:
iR1 = 40 / 12 = 3,3333... A
iR2 = 0 A
iR3 = 40 / 25 = 1,6 A
Ex8)
Resolução:
Divisor de corrente
Corrente procurada
i = (Corrente da fonte x corrente no resistor que eu não quero) / (resistor que não quero + resistor que eu quero)
iR2 = ( -50 . 25) / (25 + 12) = - 33,78 = - 33,8 A
iR1 = (- 50 . 12) / (12 + 25) = - 16,22 A
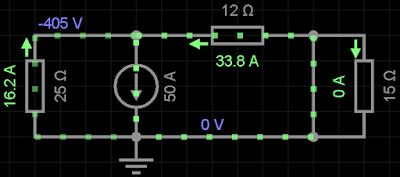 |
| Simulador EveryCircuit |
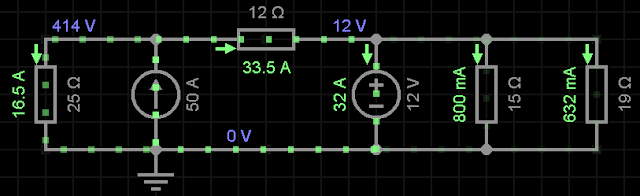
Ex9)
Resolução:
Divisor de corrente para fonte de 12V
iR2 = 12 / 15 = 0,8A
iR4 = 12 / 19 = 0,631A
Para fonte de 50A com resistor de 25Ω e 12Ω o método por divisor de corrente já não se aplica, o mais adequado seria usar o método da análise de malhas ou um outro qualquer.
 |
| Simulador EveryCircuit |
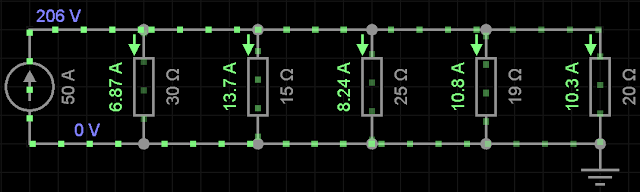
Ex10)
Resolução:
Req = 4,12Ω
i = V / Req V = i . Req = 50 . 4,12 = 206V
iR1 = 206 / 30 = 6,87A
iR2 = 206 / 15 = 13,7A
iR3 = 206 / 25 = 8,24A
iR4 = 206 / 19 = 10,8A
iR5 = 206 / 20 = 10,3A
 |
| Simulador EveryCircuit |
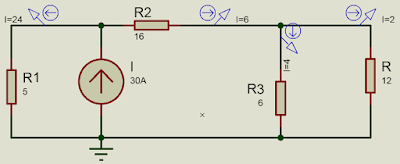
Ex11)
Resolução:
Req = 16 + (6 . 12 / (6+12)) = 20Ω
Divisor de corrente
Corrente procurada
Corrente i = (fonte corrente x res que eu não quero) / (res que eu não quero + res que eu quero)
iR1 = 30. 20 / (20+5) = 24A
iR2 = 30 . 5 / (5+20) = 6A
iR3 = 6 . 12 / (6+12) = 2A
iR = 6 . 6 / (12+6) = 4A
Obs: No resistor de 6Ω e 12Ω só possível aplicar o divisor de corrente se for um fonte isolada com apenas uma fonte corrente ou tensão, caso contrário é preciso usar outro método.
 |
| Simulador Proteus 8.6 |
Palavras chave:
Vermogensverdeler
Kragverdeler
Leistungsteiler
مقسم الطاقة
Power divider
бягучы Дзельнік
Разделител на мощността
Wopatula mphamvu
功率分配器
Razdjelnik snage
מחלק כוח
Vermogensverdeler
Power divider
Güç bölücü
21/12/2018
Switch case com letra maiúscula ou minuscula
/*Faca um algoritmo que pergunte em que turno você estuda e imprima
o horário que ele estuda. O algoritmo deve deve atender o requisito
dos caracteres tanto para maiúsculo quanto para minusculo, ambos devem
atender o solicitado.*/
import java.util.Scanner;
public class Main
{
public static void main(String[] args) {
Scanner leia = new Scanner(System.in);
System.out.print("Digite o turno que você estuda: ");
String turno = leia.nextLine();//lE UMA LINHA INTEIRA
switch(turno){
case "m":
case "M": System.out.println("Matutino");break;
case "v":
case "V": System.out.println("Vespertino");break;
case "n":
case "N": System.out.println("Noturno");break;
default: System.out.println("Valor inválido:");
}
}
}
o horário que ele estuda. O algoritmo deve deve atender o requisito
dos caracteres tanto para maiúsculo quanto para minusculo, ambos devem
atender o solicitado.*/
import java.util.Scanner;
public class Main
{
public static void main(String[] args) {
Scanner leia = new Scanner(System.in);
System.out.print("Digite o turno que você estuda: ");
String turno = leia.nextLine();//lE UMA LINHA INTEIRA
switch(turno){
case "m":
case "M": System.out.println("Matutino");break;
case "v":
case "V": System.out.println("Vespertino");break;
case "n":
case "N": System.out.println("Noturno");break;
default: System.out.println("Valor inválido:");
}
}
}
16/12/2018
Economia
Marque V (verdadeira) ou F (falsa).
a) ( F ) A empresa, desejando maximizar seus lucros, escolherá o nível de produção para o qual a diferença entre a Receita Marginal e o Custo Marginal seja a maior possível.
b) ( F ) Ao se dobrar os fatores de produção e a quantidade obtida do produto dobrar, temos rendimentos crescentes de escala.
c) ( V ) O formato das curvas de custos médio e marginal, no curto prazo, está relacionado à lei dos custos crescentes e também à lei dos rendimentos decrescentes da produção.
d) ( V ) A lei dos rendimentos decrescentes da produção ocorre somente no curto prazo, uma vez que existe um fator de produção que é fixo, no geral, é o capital.
e) ( V ) Em mercados de concorrência perfeita existem muitas firmas atuando e estas são formadoras de preços, ou seja, uma firma sozinha não afeta o preço de equilíbrio e nem a oferta isoladamente.
f) ( V ) Os custos de oportunidade são custos implícitos, porque eles são internos ao processo de produção.
g) ( V ) Uma das principais funções do CADE é observar/fiscalizar o mercado para evitar a formação de monopólios e permitir a concorrência leal entre as firmas.
h) ( V ) O surgimento de um monopólio pode estar relacionado, por exemplo, ao tamanho reduzido de um mercado e mesmo aos mecanismos de proteção à inovação.
a) ( F ) A empresa, desejando maximizar seus lucros, escolherá o nível de produção para o qual a diferença entre a Receita Marginal e o Custo Marginal seja a maior possível.
b) ( F ) Ao se dobrar os fatores de produção e a quantidade obtida do produto dobrar, temos rendimentos crescentes de escala.
c) ( V ) O formato das curvas de custos médio e marginal, no curto prazo, está relacionado à lei dos custos crescentes e também à lei dos rendimentos decrescentes da produção.
d) ( V ) A lei dos rendimentos decrescentes da produção ocorre somente no curto prazo, uma vez que existe um fator de produção que é fixo, no geral, é o capital.
e) ( V ) Em mercados de concorrência perfeita existem muitas firmas atuando e estas são formadoras de preços, ou seja, uma firma sozinha não afeta o preço de equilíbrio e nem a oferta isoladamente.
f) ( V ) Os custos de oportunidade são custos implícitos, porque eles são internos ao processo de produção.
g) ( V ) Uma das principais funções do CADE é observar/fiscalizar o mercado para evitar a formação de monopólios e permitir a concorrência leal entre as firmas.
h) ( V ) O surgimento de um monopólio pode estar relacionado, por exemplo, ao tamanho reduzido de um mercado e mesmo aos mecanismos de proteção à inovação.
12/12/2018
11/12/2018
Semáforo utilizando Demultiplexador
 |
| Semáforo utilizando Demux feito no Logisim 2.7 |
Clique aqui para fazer o download do arquivo feito no logisim
Palavras chave:
Semaphore using Demultiplexer
Semáforo utilizando Demultiplexador
Semaphore duke përdorur Demultiplexer
Semaphore gebruik Demultiplexer
Semaphor mit Demultiplexer
إشارة باستخدام Demultiplexer
Semaphore gamit ang Demultiplexer
디멀티플렉서를 사용하는 세마포어
Semaphore käyttäen Demultiplexeria
Sémaphore utilisant Demultiplexer
סמפור באמצעות Demultiplexer
Semaphore using Demultiplexer
Semaforo con demultiplexer
Lux usura Demultiplexer
Семафор с использованием демультиплексора
Seapapráid ag baint úsáide as Déantúiscéoltóir
Semaphore með Demultiplexer
Semaphore kwa kutumia Demultiplexer
Semaphore ใช้ Demultiplexer
Semaphore pomocí Demultiplexeru
Demultiplexer kullanarak Semaphore
Semafoor met Demultiplexer
08/12/2018
Multiplexador com contadores e registradores no Logsim
 |
| Multiplexador e registradores feito no Logisim 2.7 |
Clique aqui para fazer o download do arquivo feito no Logisim
Palavras chave:
Multiplexer with counters and loggers in Logsim
Multiplexor con contadores y registradores en Logsim
Multiplexer met tellers en loggers in Logsim
Multiplexer mit Zählern und Loggern in Logsim
معدد مع العدادات وقطع الاشجار في Logsim
ಲಾಗ್ಸಿಮ್ನಲ್ಲಿ ಕೌಂಟರ್ ಮತ್ತು ಲಾಗರ್ಸ್ನೊಂದಿಗೆ ಮಲ್ಟಿಪ್ಲೆಕರ್
Logsim中帶有計數器和記錄器的多路復用器
Multiplexer bi counters û loggers li Logsim
Multiplexeur avec compteurs et enregistreurs dans Logsim
מרבב עם דלפקים ולוגרים ב Logsim
ലോഗ്സെമിംഗിൽ കൗണ്ടറുകളും ലോജറുകളും ഉപയോഗിച്ച് മൾട്ടിപ്ലക്സർ
Logsim मा काउन्टरहरू र लगगहरूसँग बहुविधकर्मी
Multiplekser z licznikami i rejestratorami w Logsim
Мультиплексор со счетчиками и регистраторами в Logsim
Multiplexer s čítačkami a záznamníky v systému Logsim
02/12/2018
Multiplexador e Demultiplexador
Multiplexador e Demultiplexador no Logisim
 |
| Circuito elaborado no Logisim 2.7 |
Clique aqui para fazer o download do arquivo feito no Logisim 2.7
Palavras chave:
Multiplexer and Demultiplexer in Logisim
Multiplexer och Demultiplexer i Logisim
Multiplexer en Demultiplexer in Logisim
Multiplexer und Demultiplexer in Logisim
معدد و Demultiplexer في Logisim
Multiplexor i demultiplexor a Logisim
Logisim中的複用器和解復用器
Logisim의 멀티플렉서 및 디멀티플렉서
Multiplekser i Demultiplekser u Logisimu
Multiplexor y Demultiplexador en Logisim
Multiplexer at Demultiplexer sa Logisim
Multiplexer and Demultiplexer ann an Logisim
Πολυπλέκτης και Demultiplexer στο Logisim
Hoʻonui Multiplexer a me Demultiplexer ma Logisim
Na-agbanwe ọtụtụ na Demultiplexer na Logisim
Мультиплексор и демультиплексор в Logisim
Multiplexer iyo Demultiplexer ee Logisim
Multiplexer และ Demultiplexer ใน Logisim
Мультиплексор і Демультиплексор в Logisim
Multiplexer và Demultiplexer trong Logisim
24/11/2018
Algoritmo Método de Newton-Rapson C/C++
#include <stdio.h>
#include <math.h>
double f(double a){ //Funcao
return (pow(M_E,-a)-a);
}
//M_E = epsilon
double df(double a){ // Derivada da funcao
return (-pow(M_E,-a))-1;
}
void metodo (double x, double error, int iteracao){ //metodo
double y, errorAtual;
int i = 0;
printf("\n|%-3s|%-13s|%-21s|\n","i","valor de x ", "Erro Aproximado");
do{
i++;
y = x-(f(x)/df(x));//calculo no novo x
errorAtual = fabs((y - x)/y) * 100;//calculo do erro
x = y;
if(i > iteracao){ //verifica as interacoes
printf("Nao foi encontrada raiz dentro do numero dessas interacoes\n ");
return 0;
}else{
printf("|%-3d| %.10lf| %.14lf\t|\n", i, x, errorAtual);
}
}while (errorAtual >= error);
printf("\n\nRaiz = %f \n", x);
}
void main(){
metodo(0,0.0001, 15); //Chama o metodo ja passando os parametros
// valor do x, precisão, numero máximo de interações
}
16/11/2018
Contador síncrono tipo D crescente
Saídas
Clique aqui para fazer o download do arquivo feito no Logisim 2.7
Palavras chave:
D-type synchronous counter
Contador síncrono tipo D creciente
D-tipe sinchrone toonbank
D-Typ synchroner Zähler
نوع D متزامن عداد
сінхронны лічыльнік тыпу D вырошчванне
D sinhroni brojač
Comptador síncron de tipus D
D型同步計數器
D 형 동기 카운터
D sinhroni števec
Compteur synchrone de type D
ד סוג סינכרוני הדלפק
Cuntar sioncrónach D-cineál
Д-тип синхрони бројач
D-type синхрон тоологч
Synkron räknare av D-typ
12/11/2018
Economia
1) Marque V ou F.
a. ( V ) Bens de Giffen são uma exceção á lei da demanda, indicando uma relação direta entre o preço do bem e sua quantidade demandada.
b. ( F ) Nos sistemas econômicos socialistas, os preços são determinados pelo estado nas interações de demanda e oferta no livre mercado.
Oferta de livre mercado ocorre por trocas que ocorrem na sociedade, no sistema socialista isto não é comum
c. ( F ) Quando há avanços tecnológicos no processo produtivo, ceteris paribus, a oferta da firma tende aumentar. Neste caso, na representação gráfica da curva de oferta, esta curva se desloca para esquerda.
Se há avanços tecnológicos em favor da produção consequentemente a quantidade irá aumentar, então ela deslocará para a direita
d. ( F ) No fluxo circular da renda, a remuneração do fator de produção capital é o lucro.
O fluxo circular está em função da igualdade entre produto, renda e despesa.
e. ( V ) No equilíbrio de mercado, não há escassez e nem excedentes de bens e serviços.
f. ( F ) A utilidade marginal do consumidor é crescente, porque a medida que ele consome mais de um bem, sua satisfação aumenta.
É decrescente, à medida que mais se mais se consome um bem sua satisfação diminui
g. ( V ) O preço da celulose aumentou e como consequência os custos de se produzir o papel também aumentaram. Considerando ceteris paribus, é provável que a oferta aumente no mercado.
h. ( V ) Café e leite são bens de complementares. Se o preço do café aumentar, a quantidade demandada de leite vai diminuir, admitindo tudo mais constante.
i. ( F ) Nos sistemas econômicos socialistas a resolução dos problemas econômicos fundamentais passa pelo controle do Estado visando sempre a eficiência econômica.
Eficiência econômica não é algo se se visa como prioridade
j. ( F ) No fluxo circular da renda, a remuneração do fator de produção capital é o lucro.
A remuneração do capital é a taxa de juros já o lucro é a remuneração do empreendedor na capacidade de empreender a utilizar o capital
A remuneração do capital é a taxa de juros já o lucro é a remuneração do empreendedor na capacidade de empreender a utilizar o capital
O fluxo circular da renda está em função da igualdade entre produto, renda e despesa, portanto juros é a remuneração do capital
k. ( F ) Considere um bem normal X, partindo de uma situação de equilíbrio de mercado, se o preço do produto substituto Y diminuir, coeteris paribus, haverá um aumento no preço e na quantidade de equilíbrio relativos ao bem X.
l. ( V ) A curva de transformação de uma determinada nação poderá se descolar para a esquerda, sinalizando uma redução da possibilidade de produção, por exemplo,caso ocorra um desastre natural na nação.
m. ( F ) Se os custos de produção de um determinado setor diminuírem, tudo mais constante, a oferta desse setor deve aumentar. Em uma representação gráfica, a curva de oferta se deslocará para esquerda (cima).
A oferta se desloca para a direita
n. ( F ) A utilidade marginal dos consumidores é crescente, indicando que o consumidor sempre prefere mais a menos do bem.
É decrescente a medida que mais se consome um bem sua satisfação diminui
o. ( F ) Bens considerados de demanda elástica, apresentam uma grande variação da quantidade demandada diante de uma variação da renda dos consumidores.
É diante da variação do preço
p. ( F ) Na função de demanda de um determinado bem, a elasticidade do bem é definida através do coeficiente angular da função associado ao preço do produto.
É definido através da inclinação da reta
2) Observe o gráfico sobre equilíbrio de mercado e responda as questões abaixo:
a) O que acontece no ponto A ? Qual a tendencia dos preços nesse ponto ? Explique.
Nesse ponto houve uma falta de produto aumentando sua demanda, consequentemente os preços deverá subir até que chegue ao ponto de equilíbrio
3) Suponha o mercado de carne X. Dadas às funções de oferta e demanda por carne X, responda as questões abaixo. A renda dos consumidores é R= $80,00
Dx = 310 - 8Px + R
Qx = 190 + 3Px
a) Determine o preço (Px) e a quantidade equilíbrio (Qx) para o mercado de carne.
Resolução:
Dx = 310 - 8Px + R
Qx = 190 + 3Px
Resolução
Dx= 310 - 8Px + 80 = 390 - 8Px
Dx = Qx
390 - 8Px = 190 + 3Px
Px = 200 / 11
Px = 18,18
Dx = 390 - 8.18,18 = 244,55
Px = 190 + 3.18,18 = 244,54
b) Se a renda dos consumidores aumentar em 10% , qual será o novo ponto de equilíbrio (PA e QA) ? Represente graficamente essa alteração.
Resolução:
R = 80 + 80.10 / 100 = 88 R$
Dx = 310 - 8Px + R
Qx = 190 + 3Px
Resolução
Dx= 310 - 8Px + 88 = 398 - 8Px
Dx = Qx
398 - 8Px = 190 + 3Px
Px = 208 / 11
Px = 18,9
Dx = 398 - 8.18,9 = 246,8
Px = 190 + 3.18,9 = 246,7
c) Classifique a carne X de acordo com a renda dos consumidores. Justifique
ΔDx = 246,98 - 244,54 = 2,44
ΔQx = 246,7 - 244,54 = 2,16
É um bem normal, pois houve pouco aumento na variação.
a) O que acontece no ponto A ? Qual a tendencia dos preços nesse ponto ? Explique.
Nesse ponto houve uma falta de produto aumentando sua demanda, consequentemente os preços deverá subir até que chegue ao ponto de equilíbrio
3) Suponha o mercado de carne X. Dadas às funções de oferta e demanda por carne X, responda as questões abaixo. A renda dos consumidores é R= $80,00
Dx = 310 - 8Px + R
Qx = 190 + 3Px
a) Determine o preço (Px) e a quantidade equilíbrio (Qx) para o mercado de carne.
Resolução:
Dx = 310 - 8Px + R
Qx = 190 + 3Px
Resolução
Dx= 310 - 8Px + 80 = 390 - 8Px
Dx = Qx
390 - 8Px = 190 + 3Px
Px = 200 / 11
Px = 18,18
Dx = 390 - 8.18,18 = 244,55
Px = 190 + 3.18,18 = 244,54
b) Se a renda dos consumidores aumentar em 10% , qual será o novo ponto de equilíbrio (PA e QA) ? Represente graficamente essa alteração.
Resolução:
R = 80 + 80.10 / 100 = 88 R$
Dx = 310 - 8Px + R
Qx = 190 + 3Px
Resolução
Dx= 310 - 8Px + 88 = 398 - 8Px
Dx = Qx
398 - 8Px = 190 + 3Px
Px = 208 / 11
Px = 18,9
Dx = 398 - 8.18,9 = 246,8
Px = 190 + 3.18,9 = 246,7
c) Classifique a carne X de acordo com a renda dos consumidores. Justifique
ΔDx = 246,98 - 244,54 = 2,44
ΔQx = 246,7 - 244,54 = 2,16
É um bem normal, pois houve pouco aumento na variação.
05/11/2018
Contador ímpar crescente e contador par decrescente
 |
| Contar ímpar crescente e contador par decrescente |
Clique aqui para fazer o download do arquivo feito no Logisim 2.7
Palavras chave:
Odd counter increasing and counter decreasing pair
Ongeldige toonbank toenemende en teenverlagende paar
الغريب مكافحة زيادة ومواجهة الزوج تناقص
Comptador estrany augmentant i comptador de parells decreixents
奇數計數器增加和反減少對
Ulige tæller stigende og counter faldende par
Contador impar creciente y contador par decreciente
Impair compteur croissant et compteur décroissant paire
Contador impar contra aumento e contra-descenso
Nieparzysta licznik narastający i licznik malejący
Нечетный счетчик увеличивается и уменьшается падающая пара
Ojämn räknare ökar och motverkande minskande par
Tek sayaç artan ve karşı azalan çift
Số lượt truy cập lẻ tăng và giảm cặp lượt truy cập
03/11/2018
Algoritmo: Método de Newton - Raphson
#include <stdio.h>
#include <math.h>//biblioteca trigonométrica
double f(double a){ //Funcão
return (pow(M_E,-a)-a);
}
double df(double a){ // Derivada da funcao
return (-pow(M_E,-a))-1;
}
void metodo (double x, double error, int iteracao){ //metodo
double y, errorAtual;
int i = 0;
printf("\n|%-3s|%-13s|%-21s|\n","i","valor de x ", "Erro Aproximado");
do{
i++;
y = x-(f(x)/df(x)); //calculo no novo x
errorAtual = fabs((y - x)/y) * 100; // calculo do erro
printf("|%-3d| %.10lf| %.14lf\t|\n", i, x, errorAtual);
x = y;
if(i > iteracao){ //verifica as interacoes
return printf("Nao foi encontrada raiz dentro do numero dessas interacoes\n ");
}
}while (errorAtual >= error);
}
void main(){
metodo(0,0.000001, 30); //Chama o metodo ja passando os parametros valor do x, pressicao, numero maximo de interacoes
}
#include <math.h>//biblioteca trigonométrica
double f(double a){ //Funcão
return (pow(M_E,-a)-a);
}
double df(double a){ // Derivada da funcao
return (-pow(M_E,-a))-1;
}
void metodo (double x, double error, int iteracao){ //metodo
double y, errorAtual;
int i = 0;
printf("\n|%-3s|%-13s|%-21s|\n","i","valor de x ", "Erro Aproximado");
do{
i++;
y = x-(f(x)/df(x)); //calculo no novo x
errorAtual = fabs((y - x)/y) * 100; // calculo do erro
printf("|%-3d| %.10lf| %.14lf\t|\n", i, x, errorAtual);
x = y;
if(i > iteracao){ //verifica as interacoes
return printf("Nao foi encontrada raiz dentro do numero dessas interacoes\n ");
}
}while (errorAtual >= error);
}
void main(){
metodo(0,0.000001, 30); //Chama o metodo ja passando os parametros valor do x, pressicao, numero maximo de interacoes
}
01/11/2018
17/10/2018
Contador crescente e decrescente assíncrono tipo T
Contador crescente e decrescente com flip flop tipo T no Logisim
Clique aqui para fazer o download do arquivo feito no Logisim
Palavras chave:
increasing and decreasing count in Logisim
contador creciente y decreciente en Logisim
duke u rritur dhe zvogëluar numërimin në Logisim
steigende und abnehmende Anzahl in Logisim
زيادة وتقليل العد في Logisim
увеличаване и намаляване на броя на Logisim
在Logisim中增加和減少計數
Logisim의 증가 및 감소 카운트
Logisimin laskenta kasvaa ja laskee
zwiększenie i zmniejszenie liczby w Logisim
увеличение и уменьшение количества в Logisim
 |
| Circuito feito no Logisim 2.7 |
Clique aqui para fazer o download do arquivo feito no Logisim
Palavras chave:
increasing and decreasing count in Logisim
contador creciente y decreciente en Logisim
duke u rritur dhe zvogëluar numërimin në Logisim
steigende und abnehmende Anzahl in Logisim
زيادة وتقليل العد في Logisim
увеличаване и намаляване на броя на Logisim
在Logisim中增加和減少計數
Logisim의 증가 및 감소 카운트
Logisimin laskenta kasvaa ja laskee
zwiększenie i zmniejszenie liczby w Logisim
увеличение и уменьшение количества в Logisim
15/10/2018
Contador crescente e decrescente tipo T
Contador crescente e decrescente tipo T no LogiSim
Clique aqui para fazer o download do arquivo feito no LogiSim
01/10/2018
24/09/2018
Eletricidade Aplicada EA 07
1) Calcule V1, V2 e V3 com
a) os valores das fontes como mostrado,
b) os valores das fontes divididos por 2 e
c) os valores multiplicados por 2. Note como o principio da proporcionalidade se aplica em (b) e (c)..
Resposta: (a) V1=8V, V2=8V e V3=28V, (b) V1=2V, V2=4V e V3=14V, (a) V1=8V, V2=16V e V3=56V.
2) Calcule v e i usando o princípio da proporcionalidade. Resposta: V=8V, i=3A
Resolução:
Chute V1= 16 V
i1 = 16/8 = 2A
V= 2 . 4= 8V
LKT
16 + 8 - V2 = 0
V2 = 24V
i2 = 24/24 = 1A
i = 1 + 2 = 3A
V3 = 3 . 4 = 12V
LKT
24 + 12 - V4 = 0
V4 = 36V
i3 = 36/4 = 9A
iTotal = 9 + 3 = 12A
Proporção
K = REAL / CHUTE
K = 12 / 12 = 1
1 = iReal / 3
i = 3 . 1 = 3A
1 = i1 real / 2
i1 real = 2A
Vreal = i1 . 4 = 2 . 4 = 8V
3) Usando superposição, calcule v no circuito abaixo. Resposta: v=20V.
4) Usando superposição, calcule i e v no circuito abaixo. Resposta: 3A e 4V.
Analisando p/ fonte de tensão
14 = (4+6)i'
i' = 1,4A
V' = - 4 . 1,4 = - 5,6V
Analisando p/ fonte de corrente
Req = (4 . 6) / (4+ 6) = 2,4 Ω
V = 2,4 . 4 = 9,6 V
i'' = 9,6 / 6 = 1,6A
Portanto a corrente i será a soma de cada parcela
i = i' + i'' = 1,4 + 1,6 = 3A
V = V' + V'' = - 5,6 + 9,6 = 4V
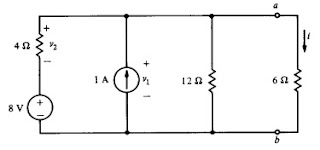
5) Substitua o circuito á esquerda dos terminais a-b pelo seu circuito equivalente de Thévenin e use este resultado para calcular i. Resposta: Voc=9V, Rth=3Ω, i=1A.
Para Rth:
Rth = (4 . 12)/ 4+12 = 3Ω
Para Voc:
Por superposição: Para fonte de 8V
Voc1 = (12 . 8) / 4 + 12 = 6V
Para fonte de 1A
4 // 12
Req = (4 . 12) / 4 + 12 = 3Ω
Voc2 = 3 . 1 = 3V
Logo;
Voc = Voc1 + Voc2 = 6 + 3 = 9V
Para i
i = Voc / (Rth + 6) = 9 / (3 + 6) = 1A
6) Substitua o circuito acima, exceto a fonte de 1A, pelo seu circuito equivalente de Thévenin e use o resultado para calcular v1. Resposta: voc=4V, Rth=2Ω, v1=6V.
Resolução:
Para Rth
1/ Rth = 1/4 + 1/12 + 1/6
Rth = 2Ω
Para Voc:
Req = (12 . 6) / 12 + 6= 4Ω
LKT
- 8 + 4i + 4i = 0
i = 1A
Voc = 4 . 1= 4V
Para V1
LKT
- V1 + 2 . 1 + 4 = 0
V1 = 6V
7) Substitua o circuito do exercício 5, exceto o resistor de 4Ω , pelo seu circuito equivalente de Norton e use o resultado para calcular v2. Resposta: isc=-1A, Rth=4Ω, v2=-2V.
Resolução:
Para Rth
Rth = 4Ω
Para isc
Req = (12 . 6) / 12+ 6= 4Ω
Para fonte de 8V
LKT
8 + 4isc1 = 0
isc1 = - 2A
Voc = 4 . 1= 4V
Para fonte de 1A
isc2 = 1A
Logo; isc = isc1 + isc2 = - 1A
8) Calcule a potência entregue a R quando
a) R = 6Ω,
b) R=2Ω e
c) quando R recebe a potência máxima.
Resposta: (a) 15,36W; (b) 14,22W; (c) 16W quando R=4Ω
Resolução:
Para Rth
Rth = (3 . 6) / (3 + 6 ) = 4Ω
Para isc da fonte de 12 V
Req = (6 . 2 ) / 6 + 2 = 1,5Ω
Divisor de tensão
V = (1,5 . 12) / (1,5 + 3) = 4V
isc1 = 4 / 2= 2A
Para fonte de 2A
Req = 3 . 6 / (3 + 6) = 2
isc2 = 2A
Logo;
isc = isc1 + isc2 = 2 + 2 = 4A
Req = (Rth . 6 )/ Rth + 6 = (4 . 6) / (4 + 6) = 2,4Ω
V = 2,4 . 4 = 9,6 V
P = V . i
P = V . V / R = (9,6 . 9,6) / 6 = 15,36W
9) Mostre que os dois circuitos abaixo são equivalentes, vistos pelos terminais a-b, e calcule a potência dissipada no resistor de 4Ω, em cada caso. Resposta (a) 9W; (b) 1W
a)
Para Rth
Rth = 4Ω
Como Rth = 4Ω em 'a' e 'b', temos que os circuitos são equivalente
Por divisor de corrente
i1 = (12 . 2) / 4 + 12 = 1,5A
P= V . i
P = R . i . i = 4 . 1,5 . 1,5 = 9W
b)
Rth = 4Ω
V = ( 4 . 8) / 4 + 12= 2V
P = V.V / R = (2 . 2) / 4 = 1 W
10) Calcule i, v1 e v2 usando a propriedade da proporcionalidade.
Resolução:
CHUTE i2 = 1/2A
V3= 1/2 . 6 = 3V
V2= 1/2 . 8 = 4V
i1 = 1/2 A
Divisor de corrente em II
i4 = ( (1/2 . 8) + 6/2 ) ) / 84 = 1/12 A
i3 = i2 + i4 = 1/2 + 1/12 = 7/12 A
Divisor de corrente em III
i5 = ( 84 . 1/12 ) / 24 = 7/24 A
i6 = i3 + i5 = 7/12 + 7/24 = 7/8 A
V6 = 7/8 . 12 = 10,5V
LKT em III
V5 + V6 - V1 = 0
24 . 7/84 + 10,5 = V1
V1 = 17,5V
i7 = 17,5 / 20 = 0,875 A
i = i6 + i7 = 7/8 + 0,875 = 1,75 A
V7 = 1,75 . 2 = 3,5V
k = REAL / CHUTE
i = (1,75) / (1/2) = 3,5 A
Calculo de i2
i2 = REAL / CHUTE
1/2 = i2REAL / 1/2
i2 Real = (1/2) / (1/2) = 1 A
V1 = V1REAL / CHUTE = 17,5 / (1/2) = 35V
V2 = 1 . 8 = 8V
11) Calcule i1 e i2 usando a propriedade da proporcionalidade. (Sugestão: faça i2=1mA, e trabalhe em direção à fonte). Resposta: i1=4mA e i2=1mA
12) Use o principio da proporcionalidade para encontrar v2. Resposta v2 = -200V
13) Calcule V usando superposição. Resposta v = 24V.
Resolução:
Para fonte de 8V
i = 8 / (8+4+12) = 0,333... mA
Para fonte de 8mA
Divisor de corrente
i1 = 8.4 / (12+8+4) = 1,333... mA
i2 = 8.20 / (20+4) = 6,666...mA
Σ das correntes
i = -1,333 + 0,333 = 1mA
i2 = 8 - 1 = 7 mA
Para fonte de 2mA
Divisor de corrente
i2 = -2.12/ (12+12) = -1mA
i1 = i2 = 1mA
Σ das correntes para fonte de 8V e 2mA
i = -1 - 1 = -2mA
i = 7 - 1 = 6mA
V = 6 . 4 = 24V
14) Calcule v usando superposição se R = 2Ω. Resposta 8V
Resolução:
Situação 1
Divisor de corrente:
Iy = 2 . 6 / (2 + 4) = 2A
V1 = 3. Iy . 6 / (3 + 6) = 4V
Situação 2
(3 + V2) / 2 = - V2/6 - V2/4
12 + 4V2 = - 2V2 + 3V2
V2 = - 12/9 = - 4/3 V
Situação 3
LKT
16 = 2 . V3 / 2 + V3 + 2 . V3/2
16 = 3V3
V3 = 16/3V
Portanto
V = V1 + V2 + V3
V = 4 - 4/3 + 16/3 = 4 + 12/3 = 8V
15) Calcule a potência máxima que pode ser entregue ao resistor R do circuito no exercício 14.
Resolução:
P/ Rht
Rth = 3 . 6 / (3+6) ] +2 = 4Ω
Para isc
i1 = -6A
LKT em i3 6(i3 - i2) + 2i3 + 16 = 0 (1)
LKT em i2 3i2 + 3+ 6(i2 - i3) = 0 (2)
i1 = - 6A
i2 = - 10/3A
isc = i1 - i3 = - 6 + 9/2 = -1,5A
i3 = - 9/2A
Por divisor de corrente
i = Rth . isc / Rth + Rth = 4(-1,5) / (4+4) = - 0,75A
P = 4 . (-0,75 . -0,75) = 2,25W
16) Calcule i usando superposição. sugestão :(Calcule i1 e i2). Resposta 6A
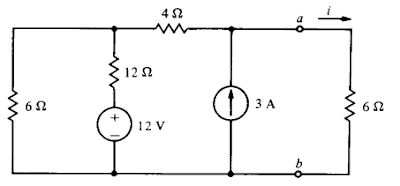
17) Substitua o circuito a esquerda dos terminais a - b pelo seu equivalente de Thévenin e use este resultado para calcular i. Resposta: Vco = 28V , Rth = 8Ω , i = 2A.
Resolução:
P/ Rth
Rth = (6 . 12) / 6 + 12) = 8Ω
P/ Voc
Para fonte de 12V:
Por divisor de tensão
Voc1 = 6 . 12 / (6 + 12) = 4V
Para fonte de 3A
Req = 6 . 12 / (6 + 12) = 4Ω
Voc2 = (4 + 4)3 = 24V
Logo; Voc = Voc1 + Voc2 = 4 + 24 = 28V
i = Voc / (Rth + 6) = 28 / (8+6) = 2A
18) Substitua o circuito do exercício 17 , exceto o resistor de 4Ω pelo seu equivalente de Thévenin e use este resultado para calcular a potência entregue pelo resistor de 4Ω. Resposta Vco = 14V , Rth=10 Ω , P = 4W.
Resolução:
Para Rth
Rth = [(6 . 12) / (6+12 ) ] +6 = 10Ω
Para Voc da fonte de 12V
Por divisor de tensão
Voc1= (6 . 12) / 6+12 = 4V
Para fonte de 3A
Voc2 = 6 . 3 = 18V
Logo;
Voc = Voc1 + Voc2 = - 4 + 18 = 14V
i = Voc / (Rth + 4) = 14 / (10 + 4) = 1A
P = V . i 2= 4 . 12 = 4W
19) Calcule v pela substituição de tudo, menos o resistor de 4Ω, pelo seu equivalente de Théveni. Resposta : v= 2V.
Resolução:
P/ Rht
Rth = 6 + 2 = 8Ω
P/ fonte de 4A
Voc1 = 6 . 4 = 24V
P/ fonte de 15A
Voc2 = 2 . 15 = 30V
P/ fonte de 6A
Voc3 = 8 . 6 = 48V
Logo; Voc + 24 + 30 -48 = 0
Voc = 6V
Por divisor de tensão:
v = 4 . Voc / (4 + Rth) = 4 . 6 / (4 + 8) = 2V
20) Calcule o equivalente de Norton, do circuito á esquerda dos terminais a - b, e use o resultado para calcular i. Resposta: isc = 2,9A , Rth = 5Ω , i = 1A.
Resolução:
P/ Rht
Req1 = 30 . 6 / (30 + 6) = 5Ω
Rth =[5 + 5].10 / ( 5+ 5 + 10) = 5Ω
P/ isc
LKT em i1 : -24 + 30(i1 - i2) + 6(i1 - i3) = 0
LKT em i2 : 10i2 + 5(i2 - i3) + 30(i2 - i1) = 0
LKT em i3 : 5(i3 - i2) + 6(i3 - i1) = 0
i1 = 47/15 A , i2 = 12/5 A , i3 = 14/5 A
isc = i3 = 2,8A
Por divisor de corrente
i = Rth . isc / (9 + Rth) = (5 . 2,8) / 5+9 = 1A
21) Calcule o equivalente de Norton, do circuito á esquerda dos terminais a -b, e use o resultado para calcular v.
Resolução:
P/ Rht
Rht = 5 + [ 30 . 6 / (30 + 6)] = 10Ω
Para isc
i1 = 3A
LKT em i2 : 20i2 + 6(i2 - i3) + 10(i2 - i1) = 0
LKT em i3 : 5(i3 - i1) + 6(i3 - i2) = 0
i2 = 7/6A , i3 = 2A , isc = i3 = 2A
Por divisor de corrente
i = Rth . isc / (30 + Rth) = 10 . 2 / (30 + 10) = 0,5A
v = 30 . 0,5 = 15V
22) Calcule o equivalente de Thévenin do circuito externo ao resistor de 4Ω e use o resultado para calcular i. Resposta: Voc = - 70V, Rth = 16Ω, i = - 3,5A.
Resolução:
P/ Rth
Rth = (10 . 10) / (40+10) = 16Ω
Voc = -7V,
i = -3,5A
P/ isc
LKT em i1 : 10(i1 - i3) + 24i1 = 0
LKT em i2 : 40(i2 - i3) + 12i2 = 0
LKT em i3 : -150 + 40(i3 - i2) + 10(i3 - i1)= 0
i1 = 65/24 A , i2 = 85/12 A , i3 = 221 / 24
isc = i1 - i2 = 65/24 - 85/12 = - 35/8A
Voc = Rht . isc = 16 . (-35/8) = - 70 V
i = Voc / (Rht + 4) = - 70 / (16 + 4) = - 3,5A
23) Calcule o valor de R que irá retirar a potência máxima do restante do circuito. Calcule também a potência máxima.
Resolução:
Rth = 4 + 6= 10Ω
Para isc
i1 = 2A
i2 - i3 = 3 (1)
LKT em ABCD
4i2 + 6i3 + 10 = 0 (2)
i1= 2A
i2 = 4/5 A
isc = i1 - i2 = 2 - 4/5 = 1,2 A
i3= - 11/5A
Por divisor de corrente
i = Rth . isc / (Rth + Rth) = 10 . 1,2 / (10 + 10) = 0,6A
P= R . i . i = 10 . 0,6 . 0,6 = 3,6W
24) Calcule a potência máxima que pode ser entregue a R se
(a) R= 12Ω e
b) R= 30Ω
a) os valores das fontes como mostrado,
b) os valores das fontes divididos por 2 e
c) os valores multiplicados por 2. Note como o principio da proporcionalidade se aplica em (b) e (c)..
Resposta: (a) V1=8V, V2=8V e V3=28V, (b) V1=2V, V2=4V e V3=14V, (a) V1=8V, V2=16V e V3=56V.
 |
| Circuito elaborado no site http://everycircuit.com/ |
2) Calcule v e i usando o princípio da proporcionalidade. Resposta: V=8V, i=3A
Resolução:
Chute V1= 16 V
i1 = 16/8 = 2A
V= 2 . 4= 8V
LKT
16 + 8 - V2 = 0
V2 = 24V
i2 = 24/24 = 1A
i = 1 + 2 = 3A
V3 = 3 . 4 = 12V
LKT
24 + 12 - V4 = 0
V4 = 36V
i3 = 36/4 = 9A
iTotal = 9 + 3 = 12A
Proporção
K = REAL / CHUTE
K = 12 / 12 = 1
1 = iReal / 3
i = 3 . 1 = 3A
1 = i1 real / 2
i1 real = 2A
Vreal = i1 . 4 = 2 . 4 = 8V
3) Usando superposição, calcule v no circuito abaixo. Resposta: v=20V.
 |
| Circuito feito no site http://everycircuit.com/ |
4) Usando superposição, calcule i e v no circuito abaixo. Resposta: 3A e 4V.
Analisando p/ fonte de tensão
 |
| Circuito elaborado no site easyeda.com |
14 = (4+6)i'
i' = 1,4A
V' = - 4 . 1,4 = - 5,6V
Analisando p/ fonte de corrente
 |
| Circuito elaborado no site easyeda.com |
Req = (4 . 6) / (4+ 6) = 2,4 Ω
V = 2,4 . 4 = 9,6 V
i'' = 9,6 / 6 = 1,6A
Portanto a corrente i será a soma de cada parcela
i = i' + i'' = 1,4 + 1,6 = 3A
V = V' + V'' = - 5,6 + 9,6 = 4V
 |
| Circuito feito no site http://everycircuit.com/ |
5) Substitua o circuito á esquerda dos terminais a-b pelo seu circuito equivalente de Thévenin e use este resultado para calcular i. Resposta: Voc=9V, Rth=3Ω, i=1A.
Para Rth:
Rth = (4 . 12)/ 4+12 = 3Ω
Para Voc:
Por superposição: Para fonte de 8V
Voc1 = (12 . 8) / 4 + 12 = 6V
Para fonte de 1A
4 // 12
Req = (4 . 12) / 4 + 12 = 3Ω
Voc2 = 3 . 1 = 3V
Logo;
Voc = Voc1 + Voc2 = 6 + 3 = 9V
Para i
i = Voc / (Rth + 6) = 9 / (3 + 6) = 1A
6) Substitua o circuito acima, exceto a fonte de 1A, pelo seu circuito equivalente de Thévenin e use o resultado para calcular v1. Resposta: voc=4V, Rth=2Ω, v1=6V.
Resolução:
Para Rth
1/ Rth = 1/4 + 1/12 + 1/6
Rth = 2Ω
Para Voc:
Req = (12 . 6) / 12 + 6= 4Ω
LKT
- 8 + 4i + 4i = 0
i = 1A
Voc = 4 . 1= 4V
Para V1
LKT
- V1 + 2 . 1 + 4 = 0
V1 = 6V
7) Substitua o circuito do exercício 5, exceto o resistor de 4Ω , pelo seu circuito equivalente de Norton e use o resultado para calcular v2. Resposta: isc=-1A, Rth=4Ω, v2=-2V.
Resolução:
Para Rth
Rth = 4Ω
Para isc
Req = (12 . 6) / 12+ 6= 4Ω
Para fonte de 8V
LKT
8 + 4isc1 = 0
isc1 = - 2A
Voc = 4 . 1= 4V
Para fonte de 1A
isc2 = 1A
Logo; isc = isc1 + isc2 = - 1A
8) Calcule a potência entregue a R quando
a) R = 6Ω,
b) R=2Ω e
c) quando R recebe a potência máxima.
Resposta: (a) 15,36W; (b) 14,22W; (c) 16W quando R=4Ω
Resolução:
Para Rth
Rth = (3 . 6) / (3 + 6 ) = 4Ω
Para isc da fonte de 12 V
Req = (6 . 2 ) / 6 + 2 = 1,5Ω
Divisor de tensão
V = (1,5 . 12) / (1,5 + 3) = 4V
isc1 = 4 / 2= 2A
Para fonte de 2A
Req = 3 . 6 / (3 + 6) = 2
isc2 = 2A
Logo;
isc = isc1 + isc2 = 2 + 2 = 4A
Req = (Rth . 6 )/ Rth + 6 = (4 . 6) / (4 + 6) = 2,4Ω
V = 2,4 . 4 = 9,6 V
P = V . i
P = V . V / R = (9,6 . 9,6) / 6 = 15,36W
9) Mostre que os dois circuitos abaixo são equivalentes, vistos pelos terminais a-b, e calcule a potência dissipada no resistor de 4Ω, em cada caso. Resposta (a) 9W; (b) 1W
a)
Para Rth
Rth = 4Ω
Como Rth = 4Ω em 'a' e 'b', temos que os circuitos são equivalente
Por divisor de corrente
i1 = (12 . 2) / 4 + 12 = 1,5A
P= V . i
P = R . i . i = 4 . 1,5 . 1,5 = 9W
b)
Rth = 4Ω
V = ( 4 . 8) / 4 + 12= 2V
P = V.V / R = (2 . 2) / 4 = 1 W
10) Calcule i, v1 e v2 usando a propriedade da proporcionalidade.
Resolução:
CHUTE i2 = 1/2A
V3= 1/2 . 6 = 3V
V2= 1/2 . 8 = 4V
i1 = 1/2 A
Divisor de corrente em II
i4 = ( (1/2 . 8) + 6/2 ) ) / 84 = 1/12 A
i3 = i2 + i4 = 1/2 + 1/12 = 7/12 A
Divisor de corrente em III
i5 = ( 84 . 1/12 ) / 24 = 7/24 A
i6 = i3 + i5 = 7/12 + 7/24 = 7/8 A
V6 = 7/8 . 12 = 10,5V
LKT em III
V5 + V6 - V1 = 0
24 . 7/84 + 10,5 = V1
V1 = 17,5V
i7 = 17,5 / 20 = 0,875 A
i = i6 + i7 = 7/8 + 0,875 = 1,75 A
V7 = 1,75 . 2 = 3,5V
k = REAL / CHUTE
i = (1,75) / (1/2) = 3,5 A
Calculo de i2
i2 = REAL / CHUTE
1/2 = i2REAL / 1/2
i2 Real = (1/2) / (1/2) = 1 A
V1 = V1REAL / CHUTE = 17,5 / (1/2) = 35V
V2 = 1 . 8 = 8V
 |
| Circuito elaboraborado por everycircuit.com/ |
11) Calcule i1 e i2 usando a propriedade da proporcionalidade. (Sugestão: faça i2=1mA, e trabalhe em direção à fonte). Resposta: i1=4mA e i2=1mA
 |
| Circuito elaborado no site http://everycircuit.com/ |
12) Use o principio da proporcionalidade para encontrar v2. Resposta v2 = -200V
13) Calcule V usando superposição. Resposta v = 24V.
Resolução:
Para fonte de 8V
Para fonte de 8mA
Divisor de corrente
i1 = 8.4 / (12+8+4) = 1,333... mA
i2 = 8.20 / (20+4) = 6,666...mA
Σ das correntes
i = -1,333 + 0,333 = 1mA
i2 = 8 - 1 = 7 mA
Para fonte de 2mA
i2 = -2.12/ (12+12) = -1mA
i1 = i2 = 1mA
Σ das correntes para fonte de 8V e 2mA
i = -1 - 1 = -2mA
i = 7 - 1 = 6mA
V = 6 . 4 = 24V
14) Calcule v usando superposição se R = 2Ω. Resposta 8V
Resolução:
Situação 1
Divisor de corrente:
Iy = 2 . 6 / (2 + 4) = 2A
V1 = 3. Iy . 6 / (3 + 6) = 4V
Situação 2
(3 + V2) / 2 = - V2/6 - V2/4
12 + 4V2 = - 2V2 + 3V2
V2 = - 12/9 = - 4/3 V
Situação 3
LKT
16 = 2 . V3 / 2 + V3 + 2 . V3/2
16 = 3V3
V3 = 16/3V
Portanto
V = V1 + V2 + V3
V = 4 - 4/3 + 16/3 = 4 + 12/3 = 8V
15) Calcule a potência máxima que pode ser entregue ao resistor R do circuito no exercício 14.
Resolução:
P/ Rht
Rth = 3 . 6 / (3+6) ] +2 = 4Ω
Para isc
i1 = -6A
LKT em i3 6(i3 - i2) + 2i3 + 16 = 0 (1)
LKT em i2 3i2 + 3+ 6(i2 - i3) = 0 (2)
i1 = - 6A
i2 = - 10/3A
isc = i1 - i3 = - 6 + 9/2 = -1,5A
i3 = - 9/2A
Por divisor de corrente
i = Rth . isc / Rth + Rth = 4(-1,5) / (4+4) = - 0,75A
P = 4 . (-0,75 . -0,75) = 2,25W
16) Calcule i usando superposição. sugestão :(Calcule i1 e i2). Resposta 6A
17) Substitua o circuito a esquerda dos terminais a - b pelo seu equivalente de Thévenin e use este resultado para calcular i. Resposta: Vco = 28V , Rth = 8Ω , i = 2A.
Resolução:
P/ Rth
Rth = (6 . 12) / 6 + 12) = 8Ω
P/ Voc
Para fonte de 12V:
Por divisor de tensão
Voc1 = 6 . 12 / (6 + 12) = 4V
Para fonte de 3A
Req = 6 . 12 / (6 + 12) = 4Ω
Voc2 = (4 + 4)3 = 24V
Logo; Voc = Voc1 + Voc2 = 4 + 24 = 28V
i = Voc / (Rth + 6) = 28 / (8+6) = 2A
18) Substitua o circuito do exercício 17 , exceto o resistor de 4Ω pelo seu equivalente de Thévenin e use este resultado para calcular a potência entregue pelo resistor de 4Ω. Resposta Vco = 14V , Rth=10 Ω , P = 4W.
Resolução:
Para Rth
Rth = [(6 . 12) / (6+12 ) ] +6 = 10Ω
Para Voc da fonte de 12V
Por divisor de tensão
Voc1= (6 . 12) / 6+12 = 4V
Para fonte de 3A
Voc2 = 6 . 3 = 18V
Logo;
Voc = Voc1 + Voc2 = - 4 + 18 = 14V
i = Voc / (Rth + 4) = 14 / (10 + 4) = 1A
P = V . i 2= 4 . 12 = 4W
19) Calcule v pela substituição de tudo, menos o resistor de 4Ω, pelo seu equivalente de Théveni. Resposta : v= 2V.
Resolução:
P/ Rht
Rth = 6 + 2 = 8Ω
P/ fonte de 4A
Voc1 = 6 . 4 = 24V
P/ fonte de 15A
Voc2 = 2 . 15 = 30V
P/ fonte de 6A
Voc3 = 8 . 6 = 48V
Logo; Voc + 24 + 30 -48 = 0
Voc = 6V
Por divisor de tensão:
v = 4 . Voc / (4 + Rth) = 4 . 6 / (4 + 8) = 2V
20) Calcule o equivalente de Norton, do circuito á esquerda dos terminais a - b, e use o resultado para calcular i. Resposta: isc = 2,9A , Rth = 5Ω , i = 1A.
Resolução:
P/ Rht
Req1 = 30 . 6 / (30 + 6) = 5Ω
Rth =[5 + 5].10 / ( 5+ 5 + 10) = 5Ω
P/ isc
LKT em i1 : -24 + 30(i1 - i2) + 6(i1 - i3) = 0
LKT em i2 : 10i2 + 5(i2 - i3) + 30(i2 - i1) = 0
LKT em i3 : 5(i3 - i2) + 6(i3 - i1) = 0
i1 = 47/15 A , i2 = 12/5 A , i3 = 14/5 A
isc = i3 = 2,8A
Por divisor de corrente
i = Rth . isc / (9 + Rth) = (5 . 2,8) / 5+9 = 1A
21) Calcule o equivalente de Norton, do circuito á esquerda dos terminais a -b, e use o resultado para calcular v.
Resolução:
P/ Rht
Rht = 5 + [ 30 . 6 / (30 + 6)] = 10Ω
Para isc
i1 = 3A
LKT em i2 : 20i2 + 6(i2 - i3) + 10(i2 - i1) = 0
LKT em i3 : 5(i3 - i1) + 6(i3 - i2) = 0
i2 = 7/6A , i3 = 2A , isc = i3 = 2A
Por divisor de corrente
i = Rth . isc / (30 + Rth) = 10 . 2 / (30 + 10) = 0,5A
v = 30 . 0,5 = 15V
22) Calcule o equivalente de Thévenin do circuito externo ao resistor de 4Ω e use o resultado para calcular i. Resposta: Voc = - 70V, Rth = 16Ω, i = - 3,5A.
Resolução:
P/ Rth
Rth = (10 . 10) / (40+10) = 16Ω
Voc = -7V,
i = -3,5A
P/ isc
LKT em i1 : 10(i1 - i3) + 24i1 = 0
LKT em i2 : 40(i2 - i3) + 12i2 = 0
LKT em i3 : -150 + 40(i3 - i2) + 10(i3 - i1)= 0
i1 = 65/24 A , i2 = 85/12 A , i3 = 221 / 24
isc = i1 - i2 = 65/24 - 85/12 = - 35/8A
Voc = Rht . isc = 16 . (-35/8) = - 70 V
i = Voc / (Rht + 4) = - 70 / (16 + 4) = - 3,5A
23) Calcule o valor de R que irá retirar a potência máxima do restante do circuito. Calcule também a potência máxima.
Resolução:
Rth = 4 + 6= 10Ω
Para isc
i1 = 2A
i2 - i3 = 3 (1)
LKT em ABCD
4i2 + 6i3 + 10 = 0 (2)
i1= 2A
i2 = 4/5 A
isc = i1 - i2 = 2 - 4/5 = 1,2 A
i3= - 11/5A
Por divisor de corrente
i = Rth . isc / (Rth + Rth) = 10 . 1,2 / (10 + 10) = 0,6A
P= R . i . i = 10 . 0,6 . 0,6 = 3,6W
24) Calcule a potência máxima que pode ser entregue a R se
(a) R= 12Ω e
b) R= 30Ω
Assinar:
Comentários (Atom)