RESISTÊNCIA DOS MATERIAIS "Módulo 7"

FÍSICA 1 P4

1) Três carrinhos de massa m1 = 4Kg, m2 = 10Kg  e m3 = 3Kg movendo -se sobre um trilho horizontal sem atrito com velocidade escalar de V1 = 5 m/s para a direita, V2 = 3 m/s para a direita e V3 = 4 m/s para a esquerda, como mostra a figura. Acopladores de velcro fazem os carrinhos se unirem após a colisão.

a) Encontre a velocidade final do conjunto de três carrinhos.

b) Qual é a variação de energia cinética do sistema ?

RESOLUÇÃO

a)

m1 * v1 + m2 * v2 + m3 * v3 = (m1 + m2 + m3) vf

4 * 5 + 10 * 3 + 3 * (-4) = (4 + 10 + 3 ) vf

vf = 2,23 m/s

b)

2) Um homem afirma que pode segurar uma criança de 12 Kg em uma colisão frontal, desde que esteja usando o cinto de segurança. Considere esse homem em uma colisão na qual ele está em um de de dois carros idênticos que andam um em direção ao outro a 30 m/s em relação ao solo. O carro no qual ele está é elevado ao repouso em 0,05s.

a) encontre o módulo da força média necessária para para segurar a criança

b) com base no resultado da parte (a) a afirmação do homem é válida ?

RESOLUÇÃO

a)

I = ΔP

I = Pf - Pi

F * Δt = m( vf - vi )

F = - (m * vi) / Δt

F = - (12 * 30) / 0,05

F = -7200 N

b)

A afirmação é falsa, a aceleração é de 600 m/s² superando a suportada pelo corpo em uma colisão ou imaginando um corpo caindo a uma aceleração de 9,8 m/s² , o homem deveria suportar uma massa de 734,7 Kg.

3) Um jogador de futebol dá um chute em uma bola de futebol de massa igual a 0,415 Kg que está em repouso. O pé do jogador está em contato com a bola durante o intervalo de tempo 0 t  0,003s, e a força do chute é dada pela expressão F(t) = [6 X 10⁶) t - (3 X 10⁹) t² ] N. Determine a intensidade das seguintes grandezas:

a) O impulso sobre a bola devido ao chute

b) A força média que o pé do jogador exerce sobre a bola durante o período de contato

c) A velocidade da bola imediatamente depois que ela perde contato com o pé do jogador

RESOLUÇÃO

a)

b)

I = Fa * Δt

9 = Fa * 0,003

Fa = 3 KN

c)

I = ΔP

I = m * v

9 = 0,45 * V

V = 20 m/s

4) Um avião modelo com massa 0,75 Kg é preso ao chão por um fio de modo que voe em um circulo horizontal de raio 30 m. O motor do avião proporciona uma força resultante de 0,8 N perpendicular ao fio de amarração

a) Encontre o torque produzido pela força resultante em relação ao centro do círculo (I = m²)

b) Encontre a aceleração translacional do avião tangente á sua trajetória do vôo.

RESOLUÇÃO

a)

F = m * a

F = m * r * α

α = F / (m * r)

b)

F = m * a

0,8 = 0,75 * a

a = 1,07 m/s²

5) A combinação de uma força aplicada e da força de atrito produz um torque total constante de 36 N.m no sentido horário sobre uma roda girando em relação a um eixo fixo. A força aplicada atua por 6s. Durante esse tempo, a velocidade angular da roda aumenta de 0 para 12 rad/s. A força aplicada é removida, e a roda chega ao repouso em 60s, encontre:

a) O momento de inércia da roda e a energia cinética rotacional após 6s

b) O torque produzido pelo atrito

RESOLUÇÃO

a)

α = ΔW / ΔT

α = 12 / 6

α = 2 rad/s

t = I * α 

36 = I * 2

I = 18 Kg/m²

b)

W = W0  + α * t

0 = 12 + α * 60

a = -0,2 rad/s²

t = I * α

t = 18 * (-0,2)

t = -3,6 N.m


6) Astronautas estão jogando beisebol na Estação Especial Internacional. Um astronauta com massa de 60 Kg inicialmente em repouso, se prepara para rebater com um taco uma bola de beisebol que está se movendo inicialmente com uma velocidade de 35 m/s área a esquerda. Após ser rebatida, ela retorna com velocidade de 45 m/s. A massa da bola é de 0,3 Kg.

a) Qual o impulso da força exercida pelo taco sobre a bola de beisebol ?

RESOLUÇÃO

I = ΔP
I = (0,3 . 45) - ( - 0,3 . 35)
I = 24 N.s

b) Qual é a velocidade de recuo do astronauta ?

RESOLUÇÃO

I = ΔP
- 24 N.s = 60 . Vf

Vf = - 0,4 m/s 

Resistência dos materiais "Módulo 6"

CARGA AXIAL - AXIAL SISTEMA ESTATICAMENTE INDETERMINADOS

O cilindro de aço tem núcleo de alumínio.As extremidades estão sujeitas a força axial de 300kN, conforme figura. Determine a tensão no aço.

Sabe-se: Cilindro de aço:

Diâmetro externo: 100 mm

Diâmetro interno: 80 mm

Eaço = 200 GPa

Eal=73,1 GPa

A  carga distribuída w é suportada por 3 barras, uma de aço e duas de alumínio. Determine o valor máximo de W sabendo que: a barra se mantem na horizontal

Aaço = 450 mm²

Aal= 450 mm²

sadm aço = 180MPa

sadm al=94MPa

Eaço = 200GPa

Eal=70GPa.

Se uma haste de 100 mm de comprimento tem diâmetro de 15 mm. se uma carga de tração axial de 100 KN for aplicada a essa haste, determine a mudança em seu comprimento. E= 200 GPa

Uma barra tem 200 mm de comprimento e área de seção transversal de 7500 mm². Determine o módulo de elasticidade do material se ela for submetida a uma carga de 50 KN.

Determine o deslocamento da extremidade A em relação a extremidade C do eixo. A área tranversal é 300 mm² e E= 210000 MPa

Duas barras, cada uma feita de um material diferente, estão acoplados e foram colocadas entre duas paredes quando a temperatura era T1= 15° C . Determine a força exercida sobre os apoios quando a temperatura alcançar T2 = 25° C. As propriedades do material e a área da seção tranversa de cada barra são dadas na figura.

Determine o deslocamento F

Poste AC:

•Material aço

•Diâmetro 20 mm

•Eaço =200 GPa

Poste BD:

•Material alumínio

•Diâmetro 40 mm

•Eal = 70GPa

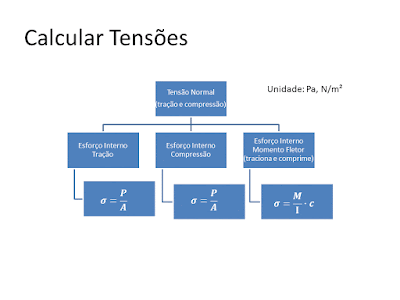
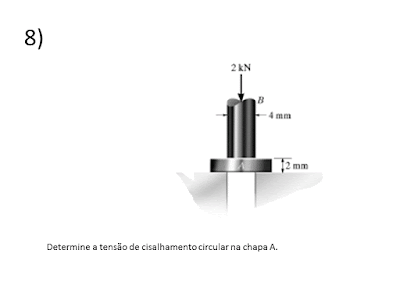
TENSÃO DE CISALHAMENTO

ÂNGULOS INTERNOS

DEFLEXÕES

Determine a ré dos seguintes azimutes
A - 39° 36' 12'
B - 128° 46' 23"
C - 249° 19' 37"
D - 323° 45' 13"

RESOLUÇÃO

A = 180° + A = 219° 36' 12"
B = 180° + B = 308° 46' 23"
C = 180° + C - 360° = 69° 19' 37"
D = 180° + D -360° = 143° 45' 13"

Converta as direções angulares: azimutes p/ Rumos

A = 46° 39' 26"  = 46 ° 39'26" NE

B= 144° 53' 35" = 35° 6' 25" SE

C= 219° 47' 19" = 39°47'19" SW

D= 289 27' 10" = 70°32' 50" NW

Calcule os ângulos internos em função dos Azimutes (sentido horário)

1-2 = 222° 32' 35"
2-3 = 317° 48' 56"
3-4 = 25° 13' 23"
4-5 = 110° 52' 45"
5-1 = 144° 44' 29"

AZi= RÉ AZ1 - AZ2

2-3 = 180 + Az 1-2 - Az 2-3 = 84° 43' 39"
3-4 = 180° Az 2-3 - Az 3-4 - 360= 112° 35' 33"
4-5 = 180° + Az 3-4 - Az 4-5 = 94° 20' 38"
5-1 = 180° + Az 4-5 - Az 5-1 = 146° 8' 16"
1-2 = 180° + Az 5-1 - Az 1-2 = 146° 8' 16"


Calcule os ângulos internos em função dos Azimutes (sentido Anti -horário)

1-2 = 290 13' 43"
2-3 = 236° 26' 54"
3-4 = 165° 18' 33"
4-5 = 100° 10' 20"
5-1 = 24° 27' 44"

2-3 = Az 2-3 - RÉ 1-2 + 180° = 126° 13' 11"
3-4 = Az 3-4 - RÉ 2-3 + 180° = 108° 51' 39"
4-5 = Az 4-5 - RÉ 3-4 + 180° = 114° 51' 47"
5-1 = Az 5-1 - RÉ 4-5 + 180° = 104° 17' 24"
1-2 = Az 1-2 - RÉ 5-1 - 180° = 85° 45' 59"

∑Az = 540° 0' 0"

Prova

Ae= 180 (n° lados - 2)
Ae = 180 (5 - 2)
Ae = 540° 0' 0'

Calcular os azimutes em função dos ângulos internos (Sentido horário) sendo Az = 46°

Ai1 = 97°
Ai2 = 92° 
Ai3 = 96°
Ai4 = 75°

Ai2 = 180° + 46° - 92° = 134°
Ai3 = 134° + 180° - 96° = 218°
Ai4 = 218° 180° - 75° = -37° + 360° = 323°
Ai1 = 323° - 180° -97° = 46°

Prova
O angulo interno Ai1 = 46°

Calcular os azimutes em função dos ângulos internos (Sentido Anti -Horário) , sendo Az = 314°

Ai1 = 96°

Ai2 = 92°

Ai3 = 97°

Ai4= 75°

Ai2 = 314 + 180 + 92= 586 - 360 = 226°

Ai3 = 226 - 180 + 97 = 143°

Ai4 = 143 + 180 + 75 = 398 - 360 = 38°

Ai1 = 38 + 180 + 96 = 314°