Elementos
armazenadores de energia - circuitos de primeira ordem
1.Um capacitor de 0,2uF tem uma carga de 10uC. Calcule a tensão e a energia. Reposta 50V, 250uJ
Resolução:
q = C.V
V = q / C = 10 / 0,2 = 50V
q = C.V
V = q / C = 10 / 0,2 = 50V
P = dw /dt
V .i = dw /dt
V .C . dV /dt = dw /dt
W = (C . V2 ) / 2 = W = ( 0,2 x 10-6 . 502 ) / 2
W = 250 uJ
V .i = dw /dt
V .C . dV /dt = dw /dt
W = (C . V2 ) / 2 = W = ( 0,2 x 10-6 . 502 ) / 2
W = 250 uJ
2. Se a energia armazenada em um capacitor de 0,5F e 25J, calcule a tensão e a carga. Resposta 10V, 5C
Resolução:
C = 0,5F W = 25J
V = ? q = ?
W = (C . V2 ) / 2 25 = (0,25 . V2 ) / 2 V = 10V
q = c . V = 0,5 . 10 = 5C
C = 0,5F W = 25J
V = ? q = ?
W = (C . V2 ) / 2 25 = (0,25 . V2 ) / 2 V = 10V
q = c . V = 0,5 . 10 = 5C
3. Dado o circuito ao lado, com C=1/4F, R1=R2=8Ω e V=40V. Se a corrente em R2 em t= 0- é 2A no sentido para baixo, calcule em t= 0- e em t= 0+:
(a) a carga no capacitor,
(b) a corrente em R1 que flui para a direita, (c) a corrente no capacitor que flui para baixo e (d) dvc / dt em [V/s]. Resposta: (a) 4C, 4C (b) 3A, 0A (c) 1A, -2A, (d) 4V/s, -8V/s
(a) a carga no capacitor,
(b) a corrente em R1 que flui para a direita, (c) a corrente no capacitor que flui para baixo e (d) dvc / dt em [V/s]. Resposta: (a) 4C, 4C (b) 3A, 0A (c) 1A, -2A, (d) 4V/s, -8V/s
Resolução:
a)
Vc(t0- )= Vc(t0+ ) ____ Capacitor não permite uma variação brusca de tensão
Vc = VR2 = 8.2 = 16V
q= C.Vc = 0,25.16 = 4C
q(t0- ) = (t0+ ) = 4C
b)
LKT: - 40 + 8i + 8.2 = 0
i = 3A
t(t0- ) _______ i1 = 3A
Vc = VR2 = 8.2 = 16V
q= C.Vc = 0,25.16 = 4C
q(t0- ) = (t0+ ) = 4C
b)
LKT: - 40 + 8i + 8.2 = 0
i = 3A
t(t0- ) _______ i1 = 3A
t0+
 |
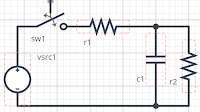| Simulador usando www.systemvision.com |
t0+____ i1 = 0A
t (0+) i = 0 A
c)
i1 = ic + iR2
ic = 3 - 2 = 1A
t (0+)
ic = -2A a corrente entra no polo negativo
t (0+) => ic = - 2A
Resolução:
Cmax = C1 + C2 + ... + C10 = 10 uF
10 capacitores de 1 uF associadas em paralelo
1/Cmin = 1/C1 + 1/C2 + ... + 1/C10
Cmin = 0,1 uF # 10 capacitores de 1 uF associados em série
5.Calcule a capacitância equivalente do circuito abaixo. Resposta: 10uF
Resolução:
C1= [(110.11) / (110+11)] = 10uF
C2= 14 + 10 = 24 uF
C1= [(110.11) / (110+11)] = 10uF
C2= 14 + 10 = 24 uF
C3= (8 . 24) / 8+24 = 6uF
C4= 6 + 6= 12 uF
Ceq = [(60 . 12) / 60+12] = 10 uF
6. Deduza uma equação para a divisão da corrente entre dois capacitores em paralelo, calculando os valores de i1 e i2.
Resolução:
C1 // C2 q1 = C1 . V i = C1. dv/dt
dv/dt = i / Cp ( 1 )
LKC i = i1 + i2 ( 2 )
i1 = C1/ dv/dt ( 3 )
q2 = C2 . V
i2 = C2 . dv/dt ( 4 )
(1) em ( 3) i1 = C1 . i / Cp
i1 = C1 . i / (C1 + C2)
(1) em (4)
i2 = C2 . i / Cp i2 = C2 . i / (C1 + C2)
C1 // C2 q1 = C1 . V i = C1. dv/dt
dv/dt = i / Cp ( 1 )
LKC i = i1 + i2 ( 2 )
i1 = C1/ dv/dt ( 3 )
q2 = C2 . V
i2 = C2 . dv/dt ( 4 )
(1) em ( 3) i1 = C1 . i / Cp
i1 = C1 . i / (C1 + C2)
(1) em (4)
i2 = C2 . i / Cp i2 = C2 . i / (C1 + C2)
7. Deduza uma equação para a divisão da tensão entre dois capacitores em serie, calculando os valores de v1 e v2.
Resolução:
Cs = C1 . C2 / (C1+C2)
V = V1 + V2 ( 1 )
q1 = C1 . V1 i = C1 . dV1 / dt
dV1 = 1 . i.dt / C1
V1 = 1/C1 ∫ t0t i . dt ( 1 )
de forma análoga para v2 e v1 temos :
8. Um indutor de 40[mH] tem uma corrente i(t) = 100 cos 10πt(t) [mA]. Calcule o enlace de fluxo e a energia em t=1/30s. Resposta: 2mWb, 50uJ.
Resolução:
L = 40 x 10-3 [ H ]
t = 1/30 [s]
i(H) = 100 . cos(10π.t) 10-3 [A]
λ = L . i = 40 x 10-3 . 100 . cos(10π.t) 10-3
λ = 40 x 10-3 . cos( 10π . 1/30) --> radiano
λ = 2 mWb
P= dw / dt
V . i = dw / dt => L . di / dt . i = dw / dt => W= L ∫ i . di
W= L . i . i / 2 = > V= L . di / dt => W= L . i . i / 2
W= 40 . 10-3[ 100. cos(10π . 1/ 30 ) 10-3] 2
W = 20 . 10-3 . 0,12 . 0,25
W = 50 uW
t = 1/30 [s]
i(H) = 100 . cos(10π.t) 10-3 [A]
λ = L . i = 40 x 10-3 . 100 . cos(10π.t) 10-3
λ = 40 x 10-3 . cos( 10π . 1/30) --> radiano
λ = 2 mWb
P= dw / dt
V . i = dw / dt => L . di / dt . i = dw / dt => W= L ∫ i . di
W= L . i . i / 2 = > V= L . di / dt => W= L . i . i / 2
W= 40 . 10-3[ 100. cos(10π . 1/ 30 ) 10-3] 2
W = 20 . 10-3 . 0,12 . 0,25
W = 50 uW
9. Um indutor de 2[mH] tem uma tensão v(t) = 2 cos 1000t(t) [V] com i(0) = 1,5A. Calcule a energia armazenada no indutor em t = π/6 ms. Resposta: 4mJ.
Resolução:
L = 2 x 10-3 H
V(t) = 2.cos(1000t) i(0) = 1,5A W = ? t = π /6
V = L. di/ dt => di = V.dt / L => i(t) - i(to) = 1/L .∫ (to, t) V .dt
i(t) = 1,5 + 1/ 10-3 ∫ (0, π /6) 2.cos(1000.t) dt => radiano
i(t) = 2A
P = dw/dt => V.i = dw/dt => L .di . i /dt = dw/dt
W = L. i 2 /2
W = 2.10-3 . 22 / 2
W = 4 mS
L = 2 x 10-3 H
V(t) = 2.cos(1000t) i(0) = 1,5A W = ? t = π /6
V = L. di/ dt => di = V.dt / L => i(t) - i(to) = 1/L .∫ (to, t) V .dt
i(t) = 1,5 + 1/ 10-3 ∫ (0, π /6) 2.cos(1000.t) dt => radiano
i(t) = 2A
P = dw/dt => V.i = dw/dt => L .di . i /dt = dw/dt
W = L. i 2 /2
W = 2.10-3 . 22 / 2
W = 4 mS
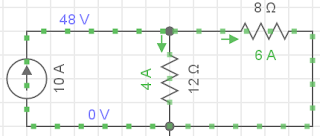
10. Dado o circuito ao lado, com I=10A, R1=12Ω, R2=8 Ω, L=1H e i1 em t =0- = 4A. Se a chave está aberta em t=0- , calcule:
(a) IL em t=0- e em t=0+,
(b) i1 em t=0+ e (c) diL / dt em [A/s].
Resposta: (a) 6A, 6A, (b) 0A, (c) -48A/s.
(a) IL em t=0- e em t=0+,
(b) i1 em t=0+ e (c) diL / dt em [A/s].
Resposta: (a) 6A, 6A, (b) 0A, (c) -48A/s.
Resolução:
a) t(0- )
a) t(0- )
 |
| Simulador EveryCircuit |
LKC em X: 4 + iL = 10
iL = 6A
Para (t0+) . O indutor não permite variação brusca de corrente
iL(0+) = iL(0+) = 6A
b)
iR1 = 0A
c)
i1 = 0 V2 = 6 . 8 = 48V
LKT em I VL + V2 + V1 = 0
VL = - 48V
V = L . di/dt di/dt = v/L = - 48/1
di/dt = - 48 A/s
11.Calcule os valores máximo e mínimo da indutância que pode ser obtida de 10 indutores de 10mH. Resposta: 100mH, 1mH
Resolução:
Lmax = l1 + l2 + ...+l10 Lmax = 10 . 10 mw
Lmáx = 100 mH 10 indutores associados em série
1/Lmin = 1/L1 + 1/L2+ ... +1/L10 1/Lmin = 10 . 1/10
Lmin = 1mH com 10 indutores associados em paralelo
12.Calcule a indutância equivalente do circuito abaixo (considerar os valores dos indutores em mH).
Resposta: 10mH
Resolução:
L1 = (3 . 6)/ (3+6 )= 2
L2 = (7+2).72 / (7+2+72)
L2 = 8
L3 = (4+8).24 / (4+8+24)
L3 = 8
Leq = 10mH
13.Deduza uma equação para a divisão da tensão entre dois indutores em serie, calculando os valores de v1 e v2.
Resposta:
Resolução:
V= L .di/dt V= Ls . di/dt di/dt = V/Ls (1)
V1 = L1 . di/dt (2)
V1 = L1 . di/dt (2)
São percorridos pelo mesmo valor da corrente
V2 = L2 . di/dt (3)
V2 = L2 . di/dt (3)
(1) em (2) V1 = L1 . V/Ls V1= L1 . V / (L1+L2)
(1) em (3) V2= L2 . V/Ls V2= L2 . V / (L1+L2)
14.Deduza uma equação para a divisão da corrente entre dois indutores em paralelo, calculando os valores de i1 e i2.
Resposta:
Resolução:
Lp= L1 . L2 / (L1+L2)
V1 // V2 => V1= V2= V
V= L1 . di1/dt => i1= 1/L2 ∫ V.dt (1)
V= L2. di2/dt => i2= 1/L2 ∫ V.dt (2)
V= L2. di/dt => i= 1/Lp ∫ V.dt ∫ V.dt = i . Lp (3)
(3) em (1) i1= 1/L1 . i . Lp
i1 = i . L1 . L2 / [L1 . (L1+L2)]
i1 = L2 . i / L1+L2
(3) em (2) i2= i . Lp / L2= i . (L1 . L2) / [L2 . (L1+L2)]
i2 = L1 . i / (L1 + L2)
15.O circuito abaixo esta em regime permanente em t = 0-. Calcule v, i1, i2, di1 / dt e di2 / dt em t=0+. Resposta: 12V, 6A, 2A, -6A/s, 0A/s
Resolução:
t(0- )
Req = 3 . 6 / (3+ 6)= 2 [Ω].
ia = 24 / (2 + 4)= 6 [A]
Divisor de corrente:
i2 = 3 . 6 / (3 + 6) = 2 [A]
*O indutor não permite a variação brusca de corrente, logo;
iL(0- )= iL(0+)
i1 = ia = 6 [A]
i2 = 2 [A]
 |
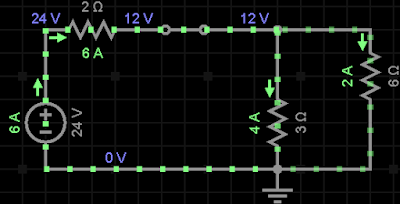| Simulador: EveryCircuit |
Para: t(0+)
LKC : 6 = 2 + i , i = 4 [A]
V = 3 . 4 = 12 [V]
LKT em i1
V1 + V = 0 , V1 = -12 [V]
V1 = L1 . di1/dt
di1/dt = -12 / 12 = - 6 [A/s]
LKT em 2
V2 + 6 . 2 - 12 = 0
V2 = 0 [V]
V2 = L2 . di2/dt = di2/dt = 0 [A/s]
16. O circuito abaixo esta em regime permanente em t = 0-. Calcule v1 e v2 em t = 0- e em t=0+.
Resposta: 5V, -20V; 25V, 20V
Resolução:
Req = ( 24 + 6).6 / ( 24 + 6 + 6) = 5Ω
(24 + 6)Ω // = 6Ω
ia = 50 / (3 + 5 +2) = 5A
V2 = 5 . 5 = 25V
i2 = 25/6 A
LCD em x
ia = i1 + i2
i1 = 5 - 25/6 = 5/6A
V1 = 6 . 5/6 = 5V
Para t(0+ )
* O indutor não permite variação brusca de corrente. Logo, iL(0- )= iL(0+ )
Req = 24(6+6) / (24 + 6 + 6) = 8Ω
V = 8 . 5 = 40V
ia = 40/24 = 5/3A
LKC em x
ia + ib = 5
ib = 5 - 5/3 = 10/3 A
V2 = 6 .ib = 6 . 10/3 = 20V
V1 = 6 (-10/3) = - 20V a corrente entra pelo lado negativo de V1
17.O circuito abaixo esta em regime permanente em t = 0-. Calcule dv1 / dt e dv2 / dt em t=0+.
Resolução:
Req = 8(12 + 6) / (8+12+6)
Req = 72/13 Ω
V = 72 . 8 /13 = 576/13 [V]
* O capacitor não permite uma variação brusca de tensão, logo:
Vc(0- ) = Vc(0+)
8Ω // V1 V1 = 576 / 13 [V]
LKT em ABCD - V1 + 12ia + 6ia = 0
18ia = 576 / 13
ia = 32 / 13 [A]
6Ω // V2
V2 = 6 . ia = 6 . 32 / 13 = 192/13 [V]
t(0+)
LKT em ix
V2 + 6(- ix) + 6( -ix) = 0
12ix = 192/13
ix = 16/13 [A]
LKT em iy
V1 - V2 + 12iy = 0
IY = 1/12 (192/13 - 576/13) = - 32/13 [A]
LKT em iz
8iz + V1 = 0
iz = (- 576 /13 ) . 1/8 = - 72 /13 [A]
Req = 72/13 Ω
V = 72 . 8 /13 = 576/13 [V]
* O capacitor não permite uma variação brusca de tensão, logo:
Vc(0- ) = Vc(0+)
8Ω // V1 V1 = 576 / 13 [V]
LKT em ABCD - V1 + 12ia + 6ia = 0
18ia = 576 / 13
ia = 32 / 13 [A]
6Ω // V2
V2 = 6 . ia = 6 . 32 / 13 = 192/13 [V]
t(0+)
LKT em ix
V2 + 6(- ix) + 6( -ix) = 0
12ix = 192/13
ix = 16/13 [A]
LKT em iy
V1 - V2 + 12iy = 0
IY = 1/12 (192/13 - 576/13) = - 32/13 [A]
LKT em iz
8iz + V1 = 0
iz = (- 576 /13 ) . 1/8 = - 72 /13 [A]
Nenhum comentário:
Postar um comentário