Eletricidade Aplicada EA 07

1) Calcule V1, V2 e V3 com
a) os valores das fontes como mostrado,
b) os valores das fontes divididos por 2 e
c) os valores multiplicados por 2. Note como o principio da proporcionalidade se aplica em (b) e (c)..

Resposta: (a) V1=8V, V2=8V e V3=28V, (b) V1=2V, V2=4V e V3=14V, (a) V1=8V, V2=16V e V3=56V.

Circuito elaborado no site http://everycircuit.com/

2) Calcule v e i usando o princípio da proporcionalidade. Resposta: V=8V, i=3A

Resolução:

Chute V1= 16 V
i1 = 16/8 = 2A

V= 2 . 4= 8V
LKT
16 + 8 - V2 = 0
V2 = 24V

i2 = 24/24 = 1A
i = 1 + 2 = 3A
V3 = 3 . 4 = 12V

LKT
24 + 12 - V4 = 0
V4 = 36V

i3 = 36/4 = 9A

iTotal = 9 + 3 = 12A

Proporção
K = REAL / CHUTE

K = 12 / 12 = 1

1 = iReal / 3
i = 3 . 1 = 3A

1 = i1 real / 2
i1 real = 2A

Vreal = i1 . 4 = 2 . 4 = 8V

3) Usando superposição, calcule v no circuito abaixo. Resposta: v=20V.

Circuito feito no site http://everycircuit.com/

4) Usando superposição, calcule i e v no circuito abaixo. Resposta: 3A e 4V.

Analisando p/ fonte de tensão

Circuito elaborado no site easyeda.com

14 = (4+6)i'
i' = 1,4A
V' = - 4 . 1,4 = - 5,6V

Analisando p/ fonte de corrente

Circuito elaborado no site easyeda.com

Req = (4 . 6) / (4+ 6) = 2,4 Ω
V = 2,4 . 4 = 9,6 V
i'' = 9,6 / 6 = 1,6A

Portanto a corrente i será a soma de cada parcela

i = i' + i'' = 1,4 + 1,6 = 3A
V = V' + V'' = - 5,6 + 9,6 = 4V

Circuito feito no site http://everycircuit.com/

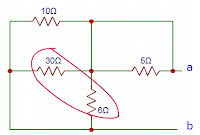
5) Substitua o circuito á esquerda dos terminais a-b pelo seu circuito equivalente de Thévenin e use este resultado para calcular i. Resposta: Voc=9V, Rth=3Ω, i=1A.

Para Rth:

Rth = (4 . 12)/ 4+12 = 3Ω

Para Voc:

Por superposição: Para fonte de 8V

Voc1 = (12 . 8) / 4 + 12 = 6V

Para fonte de 1A

4 // 12
Req = (4 . 12) / 4 + 12 = 3Ω

Voc2 = 3 . 1 = 3V

Logo;
Voc = Voc1 + Voc2 = 6 + 3 = 9V

Para i

i = Voc / (Rth + 6) = 9 / (3 + 6) = 1A

6) Substitua o circuito acima, exceto a fonte de 1A, pelo seu circuito equivalente de Thévenin e use o resultado para calcular v1. Resposta: voc=4V, Rth=2Ω, v1=6V.

Resolução:

Para Rth

1/ Rth = 1/4 + 1/12 + 1/6
Rth = 2Ω

Para Voc:

Req = (12 . 6) / 12 + 6= 4Ω

LKT
- 8 + 4i + 4i = 0
i = 1A

Voc = 4 . 1= 4V

Para V1

LKT
- V1 + 2 . 1 + 4 = 0
V1 = 6V


7) Substitua o circuito do exercício 5, exceto o resistor de 4Ω , pelo seu circuito equivalente de Norton e use o resultado para calcular v2. Resposta: isc=-1A, Rth=4Ω, v2=-2V.

Resolução:

Para Rth

Rth = 4Ω

Para isc

Req = (12 . 6) / 12+ 6= 4Ω

Para fonte de 8V

LKT

8 + 4isc1 = 0
isc1 = - 2A

Voc = 4 . 1= 4V


Para fonte de 1A

isc2 = 1A


Logo; isc = isc1 + isc2 = - 1A



8) Calcule a potência entregue a R quando
a) R = 6Ω,
b) R=2Ω e
c) quando R recebe a potência máxima.

Resposta: (a) 15,36W; (b) 14,22W; (c) 16W quando R=4Ω

Resolução:

Para Rth

Rth = (3 . 6) / (3 + 6 ) = 4Ω


Para isc da fonte de 12 V

Req = (6 . 2 ) / 6 + 2 = 1,5Ω

Divisor de tensão

V = (1,5 . 12) / (1,5 + 3) = 4V

isc1 = 4 / 2= 2A

Para fonte de 2A

Req = 3 . 6 / (3 + 6) = 2

isc2 = 2A


Logo;
isc = isc1 + isc2 = 2 + 2 = 4A

Req = (Rth . 6 )/ Rth + 6 = (4 . 6) / (4 + 6) = 2,4Ω
V = 2,4 . 4 = 9,6 V
P = V . i
P = V . V / R = (9,6 . 9,6) / 6 = 15,36W

9) Mostre que os dois circuitos abaixo são equivalentes, vistos pelos terminais a-b, e calcule a potência dissipada no resistor de 4Ω, em cada caso. Resposta (a) 9W; (b) 1W

a)
Para Rth

Rth = 4Ω

Como Rth = 4Ω em 'a' e 'b', temos que os circuitos são equivalente
Por divisor de corrente

i1 = (12 . 2) / 4 + 12 = 1,5A

P= V . i
P = R . i . i = 4 . 1,5 . 1,5 = 9W


b)

Rth = 4Ω

V = ( 4 . 8) / 4 + 12= 2V
P = V.V / R = (2 . 2) / 4 = 1 W


10) Calcule i, v1 e v2 usando a propriedade da proporcionalidade.

Resolução:

CHUTE i2 = 1/2A

V3= 1/2 . 6 = 3V
V2= 1/2 . 8 = 4V

i1 = 1/2 A

Divisor de corrente em II

i4 = ( (1/2 . 8) + 6/2 ) ) / 84 = 1/12 A

i3 = i2 + i4 =  1/2 + 1/12 = 7/12 A

Divisor de corrente em III

i5 = ( 84 . 1/12 ) / 24 = 7/24 A

i6 = i3 + i5 = 7/12 + 7/24 = 7/8 A

V6 = 7/8 . 12 = 10,5V

LKT em III

V5 + V6 - V1 = 0
24 . 7/84 + 10,5 = V1
V1 = 17,5V

i7 = 17,5 / 20 = 0,875 A

i = i6 + i7 = 7/8 + 0,875 = 1,75 A

V7 = 1,75 . 2 = 3,5V

k = REAL / CHUTE
i = (1,75) / (1/2) = 3,5 A

Calculo de i2

i2 = REAL / CHUTE
1/2 = i2REAL / 1/2
i2 Real = (1/2) / (1/2) = 1 A

V1 = V1REAL / CHUTE = 17,5 / (1/2) = 35V

V2 = 1 . 8 = 8V

Circuito elaboraborado por everycircuit.com/

11) Calcule i1 e i2 usando a propriedade da proporcionalidade. (Sugestão: faça i2=1mA, e trabalhe em direção à fonte). Resposta: i1=4mA e i2=1mA

Circuito elaborado no site http://everycircuit.com/

12) Use o principio da proporcionalidade para encontrar v2. Resposta v2 = -200V

13) Calcule V usando superposição. Resposta v = 24V.

Resolução:

Para fonte de 8V

i = 8 / (8+4+12) = 0,333... mA

Para fonte de 8mA

Divisor de corrente

i1 = 8.4 / (12+8+4) = 1,333... mA

i2 = 8.20 / (20+4) = 6,666...mA

Σ das correntes

i = -1,333 + 0,333 = 1mA
i2 = 8 - 1 = 7 mA

Para fonte de 2mA

Divisor de corrente
i2 = -2.12/ (12+12) = -1mA
i1 = i2 = 1mA

Σ das correntes para fonte de 8V e 2mA
i = -1 - 1 = -2mA
i = 7 - 1 = 6mA

V = 6 . 4 = 24V

14) Calcule v usando superposição se R = 2Ω. Resposta 8V

Resolução:

Situação 1

Divisor de corrente:
Iy = 2 . 6 / (2 + 4) = 2A

V1 = 3. Iy . 6 / (3 + 6) = 4V

Situação 2

(3 + V2) / 2 = - V2/6 - V2/4

12 + 4V2 = - 2V2 + 3V2
V2 = - 12/9 = - 4/3 V


Situação 3

LKT
16 = 2 . V3 / 2 + V3 + 2 . V3/2
16 = 3V3
V3 = 16/3V

Portanto
V = V1 + V2 + V3
V = 4 - 4/3 + 16/3 = 4 + 12/3 = 8V


15) Calcule a potência máxima que pode ser entregue ao resistor R do circuito no exercício 14.

Resolução:
P/ Rht

Rth = 3 . 6 / (3+6) ] +2 = 4Ω

Para isc

i1 = -6A
LKT em i3    6(i3 - i2) + 2i3 + 16 = 0 (1)

LKT em i2   3i2 + 3+ 6(i2 - i3) = 0  (2)

i1 = - 6A
i2 = - 10/3A

isc = i1 - i3 = - 6 + 9/2 = -1,5A
i3 = - 9/2A

Por divisor de corrente
i = Rth . isc / Rth + Rth = 4(-1,5) / (4+4) = - 0,75A

P = 4 . (-0,75 . -0,75) = 2,25W


16) Calcule i usando superposição. sugestão :(Calcule i1 e i2). Resposta 6A

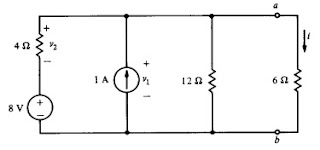
17) Substitua o circuito a esquerda dos terminais a - b pelo seu equivalente de Thévenin e use este resultado para calcular i. Resposta: Vco = 28V , Rth = 8Ω , i = 2A.

Resolução:
P/ Rth

Rth = (6 . 12) / 6 + 12) = 8Ω

P/ Voc
Para fonte de 12V:

Por divisor de tensão
Voc1 = 6 . 12 / (6 + 12) = 4V

Para fonte de 3A

Req = 6 . 12 / (6 + 12) = 4Ω

Voc2 = (4 + 4)3 = 24V
Logo; Voc = Voc1 + Voc2 = 4 + 24 = 28V

i = Voc / (Rth + 6) = 28 / (8+6) = 2A


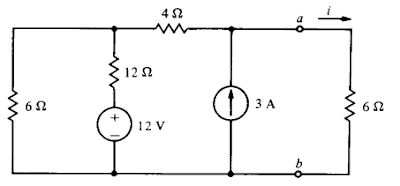
18) Substitua o circuito do exercício 17 , exceto o resistor de 4Ω pelo seu equivalente de Thévenin e use este resultado para calcular  a potência entregue pelo resistor de 4Ω. Resposta Vco = 14V ,  Rth=10 Ω , P = 4W.

Resolução:

Para Rth

Rth = [(6 . 12) / (6+12 ) ] +6 = 10Ω

Para Voc da fonte de 12V

Por divisor de tensão

Voc1= (6 . 12) / 6+12 = 4V

Para fonte de 3A

Voc2 = 6 . 3 = 18V

Logo;
Voc = Voc1 + Voc2 = - 4 + 18 = 14V

i = Voc / (Rth + 4) = 14 / (10 + 4) = 1A

P = V . i ²= 4 . 1² = 4W


19) Calcule v pela substituição de tudo, menos o resistor de 4Ω, pelo seu equivalente de Théveni. Resposta : v= 2V.

Resolução:
P/ Rht
Rth = 6 + 2 = 8Ω

P/ fonte de 4A

Voc1 = 6 . 4 = 24V
P/ fonte de 15A

Voc2 = 2 . 15 = 30V
P/ fonte de 6A

Voc3 = 8 . 6 = 48V
Logo; Voc + 24 + 30 -48 = 0
Voc = 6V

Por divisor de tensão:

v = 4 . Voc / (4 + Rth) = 4 . 6 / (4 + 8) = 2V


20) Calcule o equivalente de Norton, do circuito á esquerda dos terminais a - b, e use o resultado para calcular i. Resposta: isc = 2,9A , Rth = 5Ω , i = 1A.

Resolução:
P/ Rht

Req1 = 30 . 6 / (30 + 6) = 5Ω

Rth =[5 + 5].10 / ( 5+ 5 + 10) = 5Ω

P/ isc

LKT em i1 :  -24 + 30(i1 - i2) + 6(i1 - i3) = 0

LKT em i2 :  10i2 + 5(i2 - i3) + 30(i2 - i1) = 0

LKT em i3 :  5(i3 - i2) + 6(i3 - i1) = 0

i1 = 47/15 A   ,  i2 = 12/5 A   ,  i3 = 14/5 A
isc = i3 = 2,8A

Por divisor de corrente

i = Rth . isc / (9 + Rth) = (5 . 2,8) / 5+9 = 1A


21) Calcule o equivalente de Norton, do circuito á esquerda dos terminais a -b, e use o resultado para calcular v.

Resolução:
P/ Rht

Rht = 5 + [ 30 . 6 / (30 + 6)] = 10Ω

Para isc

i1 = 3A

LKT em i2 : 20i2 + 6(i2 - i3) + 10(i2 - i1) = 0
LKT em i3 : 5(i3 - i1) + 6(i3 - i2) = 0

i2 = 7/6A  ,  i3 = 2A   , isc = i3 = 2A

Por divisor de corrente

i = Rth . isc / (30 + Rth) = 10 . 2 / (30 + 10) = 0,5A

v = 30 . 0,5 = 15V


22) Calcule o equivalente de Thévenin do circuito externo ao resistor de 4Ω e use o resultado para calcular i. Resposta: Voc = - 70V, Rth = 16Ω, i = - 3,5A.

Resolução:
P/ Rth

Rth = (10 . 10) / (40+10) = 16Ω
Voc = -7V,
i = -3,5A

P/ isc

LKT em i1 :   10(i1 - i3) + 24i1 = 0
LKT em i2 :   40(i2 - i3) + 12i2 = 0
LKT em i3  :  -150 + 40(i3 - i2) + 10(i3 - i1)= 0

i1 = 65/24 A   ,   i2 = 85/12 A  ,     i3 = 221 / 24

isc = i1 - i2 = 65/24 - 85/12 = - 35/8A

Voc = Rht . isc = 16 . (-35/8) = - 70 V

i = Voc / (Rht + 4) = - 70 / (16 + 4) = - 3,5A

23) Calcule o valor de R que irá retirar a potência máxima do restante do circuito. Calcule também a potência máxima.

Resolução:

Rth = 4 + 6= 10Ω

Para isc

i1 = 2A
i2 - i3 = 3 (1)

LKT em ABCD
4i2 + 6i3 + 10 = 0  (2)
i1= 2A
i2 = 4/5 A

isc = i1 - i2 = 2 - 4/5 = 1,2 A

i3= - 11/5A

Por divisor de corrente
i = Rth . isc / (Rth + Rth) = 10 . 1,2 / (10 + 10) = 0,6A

P= R . i . i = 10 . 0,6 . 0,6 = 3,6W


24) Calcule a potência máxima que pode ser entregue a R se
(a) R= 12Ω e

b) R= 30Ω

Contador crescente e descrescente

CIs utilizados:

2 CIs decodificador 7447
2 CIs 74192
2 Display 7 segmentos anodo
2 Botão de pressão

Circuito elaborado no proteus 8.6

Máquina de estados tipo T

Contador síncrono crescente tipo T de 5 a F

Contador crescente de 5 a F

Tabela de estados Flip Flop JK

Tabela completa do Flip Flop JK com Preset , Enable e Clear

Tabela flip flop JK com Preset , Enable e Clear

Tabela verdade Flip Flop tipo JK com Preset e Clear

Tabela flip flop JK com Preset e Clear

Tabela flip flop tipo JK

Máquina de estados com flip flop tipo T

Contador síncrono crescente tipo T de módulo 10

Saídas feito no emulador Logisim

Contador crescente de módulo 10

Ou

Contador crescente de módulo 10

Registradores com FLIP FLOP tipo T

Máquina de estados com flip flop tipo T decrescente módulo 11

Contador decrescente módulo 11

Eletrônica Digital PF

1. Monte o circuito e explique o funcionamento de um contador síncrono decrescente de módulo 10.

Resolução:

Resolução:

Contador decrescente módulo 10

OU

Contador decrescente módulo 10

Contador síncrono decrescente JK 

CLIQUE AQUI para fazer o download do arquivo feito no Logisim

2. As formas de onda de entrada mostradas na figura 2 são aplicadas num somador de 2 bits. Determine as formas de onda para a soma e o carry de saída em relação às entradas construindo o diagrama de temporização.

Resolução:

3. Projete um circuito lógico com o DEMUX que tem a capacidade de indicar se um número pertence aos números primos. Admita que você tenha disponível apenas DEMUX com oito saídas e portas OU de três entradas. O conjunto a ser analisado é composto de números inteiros entre 0 e 31.

Resolução:

4. Converta o código Gray 1111 para binário.

Resolução:

Circuito conversor de código gray para binário

5. Para o FF da figura abaixo, desenhe a forma de onda na saída em função dos sinais aplicados.

Resolução:

Eletrônica Digital P2

1. O diagrama de estado abaixo representa o funcionamento de um contador de números. Obtenha o seu circuito no modo síncrono. Utilizar o flip-flops T.

Resolução:

Máquina de estado tipo T módulo 5

CLIQUE AQUI para fazer o download do arquivo feito no Logisim

2. Apresente a tabela verdade, a equação característica e o circuito do meio somador.

3). Projete um circuito com o MUX que tem a capacidade de indicar se um número pertence aos números de Fibonacci (0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...). Admita que você tenha disponível apenas MUX com oito entradas e o conjunto a ser analisado é composto de números inteiros entre 0 e 31.

Resolução:

4. Explique a função do conversor D/A dentro do conversor A/D.

Resolução:

O conversor analógico-digital é capaz de gerar uma representação digital a partir de uma grandeza analógica, normalmente um sinal representado por um nível de tensão ou intensidade de corrente elétrica. O circuito do conversor é composto por um contador de década que gera o código BCD 8421 nas saídas A', B', C' e D'. As saídas entram em um conversor D/A, fazendo com que apresente na saída uma tensão de referência, a qual é injetada em uma das entradas de um circuito comparador constituído por um amplificador operacional. Na outra entrada têm-se o sinal analógico a ser convertido

Os ADCs são muito úteis na interface entre dispositivos digitais (microprocessadores, microcontroladores, DSPs, etc) e dispositivos analógicos e são utilizados em aplicações como leitura de sensores, digitalização de áudio e vídeo.

Mini Teste 2

1. O diagrama de estado abaixo representa o funcionamento de um contador. Obter o seu circuito no modo assíncrono, utilizando flip - flops T.

Resolução:

CLIQUE AQUI para fazer o download do arquivo feito no Logisim

2. Preencha a tabela (coluna do código de Gray). Proponha um circuito que utiliza porta lógicas para transformar Gray em código Binário.

Resolução:

Contador síncrono JK

Contador síncrono decrescente do tipo JK

Contador síncrono decrescente com flip - flop JK

CLIQUE AQUI para fazer o download do arquivo feito no Logisim

Palavras chave:

JK型の同期カウンタの減少
JK 유형의 동기 카운터 감소
Declining synchronous counter of type JK
ตัวนับซิงโครนัสที่ลดลงของ JK ชนิด
Absenkender Synchronzähler vom Typ JK
拒絕JK型同步計數器
Nedgang synkron teller av typen JK
Contatore sincrono decrescente di tipo JK
Πτώση σύγχρονου μετρητή τύπου JK
Contador síncrono decreciente del tipo JK
Klesající synchronní čítač typu JK
إنقاص عداد متزامن من النوع J
Compteur synchrone en déclin de type JK
Pevçûnek hevpeymaniya JK-ê ya duyemîn derxistin
Сбой синхронного счетчика типа JK
Dekline synchronous vann san preskripsyon nan kalite JK

Contador Síncrono JK

CONTADOR SÍNCRONO CRESCENTE TIPO JK

Contador síncrono crescente com flip flop JK

CLIQUE AQUI para fazer o download do arquivo feito no Logisim

Palavras chave:

GROWING SYNCHRONOUS COUNTER TYPE JK
CROSSING SYNCHRONOUS COUNTER TYPE JK
TIPO DI CONTATORE SINCRONO CRESCENTE JK
BÜYÜME SENKRON SAYACI TİPİ JK
WACHSEN SYNCHRON-ZÄHLER TYP JK
نمو متزامن متزامن مع نوع JK
CINEÁL COMHARTHA SYNCHRONACH AG FÁS JK
ประเภทตัวนับแบบทวนคำ JK ของ GROWING
РОСТ СИНХРОННОГО СЧЕТА ТИПА JK
ΑΝΑΠΤΥΞΙΑΚΟΣ ΣΥΓΧΡΟΝΟΣ ΑΝΤΙΣΤΟΙΧΟΣ ΤΥΠΟΣ JK
不斷增長的同步計數器型JK
CONTADOR SÍNCRONO CRECIENTE TIPO JK
재계 동시 카운터 유형 JK
同期型カウンタ型JKの成長

Sistemas Operacionais

EXERCÍCIOS SOBRE ENTRADA E SAÍDA

1) Explique o modelo de camadas aplicado na gerência de dispositivos.

Resp : A gerência de dispositivos é estruturada através de camadas em um modelo semelhante ao apresentado para o sistema operacional como um todo. As camadas de mais baixo nível escondem características dos dispositivos das camadas superiores, oferecendo uma interface simples e confiável ao usuário e suas aplicações. As camadas são divididas em dois grupos, onde o primeiro grupo visualiza os diversos tipos de dispositivos do sistema de um modo único, enquanto o segundo é específico para cada dispositivo. A maior parte das camadas trabalha de forma independente do dispositivo.

2) Qual é a principal finalidade das rotinas de E/S?

Resp : Tornar as operações de E/S o mais simples possível para o usuário e suas aplicações. Com isso, é possível ao usuário realizar operações de E/S sem se preocupar com detalhes do dispositivo que está sendo acessado.

3) Quais as diferentes formas de um programa chamar rotinas de E/S?

Resp : Por comandos de leitura/gravação e chamadas a bibliotecas de rotinas oferecidas por linguagens de alto nível ou diretamente através de uma system call em um código de alto nível.

4) Quais as principais funções do subsistema de E/S?

Resp : Criar uma interface padronizada com os device drivers e oferecer uma interface uniforme com as camadas superiores.

5) Por que o sistema de E/S deve criar uma interface padronizada com os device drivers ?

Resp : Para que seja possível a inclusão de novos drivers sem a necessidade de alteração da camada de subsistema de E/S.

6) Explique o funcionamento da técnica de DMA e sua principal vantagem.

Resp : De forma simplificada, uma operação de leitura em disco utilizando DMA teria os seguintes passos. A UCP, através do device driver, inicializa os registradores do controlador de DMA e, a partir deste ponto, fica livre para realizar outras atividades. O controlador de DMA, por sua vez, solicita ao controlador de disco a transferência do bloco do disco para o seu buffer interno. Terminada a transferência, o controlador de disco verifica a existência de erros e, caso não haja erros, o controlador de DMA transfere o bloco para o buffer de E/S na memória principal. Ao término da transferência, o controlador de DMA gera uma interrupção avisando ao processador que o dado já encontra-se na memória principal. A principal vantagem dessa técnica é evitar que o processador fique ocupado com a transferência do bloco para a memória.

EXERCÍCIOS SOBRE MEMÓRIA VIRTUAL

1) Quais as funções básicas da gerência de memória ?

Resp : Maximizar o número de processos na memória, permitir a execução de programas maiores que a memória física, compartilhamento de dados na memória e proteção da memória utilizada por cada processo e pelo sistema operacional.

2) Considere um sistema computacional com 40Kb de memória principal e que utiliza um sistema operacional de 10Kb que implemente alocação contígua de memória. Qual a taxa de subtuilização da memória principal para um programa que ocupe 20Kb de memória?

Resp : Considerando que o sistema opeacional e o programa somados ocupam ¾ da memória principal, temos 25% de subutilização da memória.

3) Qual a diferença entre fragmentação interna e fragmentação externa da memória principal ?

Resp : Fragmentação interna ocorre em espaços livres e contíguos na memória principal que são pré-alocados por processos, não possibilitando, portanto, o uso por outros processos. Fragmentação externa ocorre em espaços livres e contínuos, porém tão pequenos que não possibilitam a alocação de programas por processos.

Contador síncrono tipo T

Contador crescente tipo T síncrono

• 
  

Números primos com Demultiplexador

Tabela de display módulo 31 com saídas dos números primos

Clique aqui para fazer o download do arquivo feito no Logisim