O principal desafio na agricultura moderna é manter e/ou aumentar a fertilidade do solo, e uma das suas funções mais importantes, como suporte para o crescimento das plantas, é fornecer nutrientes essenciais, os macronutrientes e micronutrientes.
Entretanto, o teor de nutrientes nos solos é perdido pela absorção das culturas, lixiviação e erosão do solo. Há também perdas de nutrientes (fósforo, por exemplo) por fixação nos óxidos de ferro presentes no solo, especialmente em solos altamente intemperizados.
Os nutrientes do solo são divididos em macro e micronutrientes, de acordo com o grau de utilização pelos vegetais. Macronutrientes são elementos químicos que ocorrem em níveis consideráveis em materiais vegetais ou em fluidos da planta, e são considerados os elementos: C, H, O, N, P, K, Ca, Mg e S, dos quais carbono, hidrogênio e oxigênio são obtidos a partir da atmosfera. Outros macronutrientes essenciais devem ser obtidos a partir do solo e, por isso, geralmente são adicionados como adubo.
Já os micronutrientes são os elementos essenciais em níveis muito baixos e, geralmente são necessários para o funcionamento de enzimas essenciais. São eles: Fe, Mn, B, Mo, Cu, Zn, Cl e Co. Por isso, quando a fertilidade do solo é baixa, a produtividade das culturas é incrementada com o uso de fertilizantes, até que seja alcançado um máximo, após o qual a produtividade permanece estável ou decresce.
COMPOSIÇÃO DA SOLUÇÃO DO SOLO
O conteúdo de outros elementos como Ca, Mg, Na e K, depende da quantidade desde na rocha e da lixiviação que o solo tenha sofrido, uma vez que esses compostos são solúveis em água.
O compartimento no solo, no qual os nutrientes estão disponíveis para as plantas, é denominado solução do solo.
Para Raij, a absorção de elementos químicos pelas raízes das plantas dá -se a partir da solução do solo. Segundo Campbell et al., o conhecimento da composição química da solução do solo fornece subsídios importantes para o entendimento das alterações físicas e químicas advindas do uso e manejo e para o monitoramento das várias práticas de melhoramento do solo. Pode também auxiliar nas estimativas da taxa de intemperismo, na taxa de ciclagem dos elementos químicos e no influxo e lixiviação de nutrientes no campo.
A solução no solo é fase líquida do solo que contém nutrientes dissolvidos provenientes dos processos químicos e bioquímicos do solo, da hidrosfera e da atmosfera. A solução do solo representa a fonte imediata de nutrientes às plantas.
COMO OCORRE A TROCA DE NUTRIENTES ENTRE A SOLUÇÃO DO SOLO E FASE SÓLIDA?
É um processo que depende da concentração da solução do solo, que, por sua vez, depende da solubilidade dos compostos químicos nas plantas. É tudo uma questão de equilíbrio.
Os nutrientes que se encontram adsorvidos na fase sólida mineral do solo vão sendo liberados para a solução do solo à medida que ocorre a absorção deles pelos vegetais. A capacidade do solo em suprir nutrientes às plantas está ligada ao teor do nutriente disponível na fase sólida. Por isso, há necessidade de reposição dos nutrientes da solução do solo por meio da liberação destes da fase sólida, pelo processo de intemperismo. Entretanto, essa liberação é muito lenta e depende do mineral primário predominante. Nos solos tropicais, predomina o quartzo na fração grosseira, que é um mineral muito resistente ao intemperismo e pobre em nutrientes. Outros minerais primários, como micas e feldspatos, presentes em solos mais jovens e nas camadas mais profundas, podem representar uma importante fonte de nutrientes a longo prazo.
FATORES QUE AFETAM O CRESCIMENTO E O DESENVOLVIMENTO DAS PLANTAS E A DISPONIBILIDADE DE NUTRIENTES NO SOLO.
Muitos atributos do solo, da planta, dos sistemas de manejo e do clima afetam, direta ou indiretamente, o ecodesenvolvimento dos vegetais.
Entre os fatores do solo, vamos detalhar os mais importantes:
- Textura e Estrutura - são atributos físicos do solo ligados a propriedades importantes, como densidade, espaço poroso, umidade e taxa de infiltração de água, erodibilidade e compactação. Essas propriedades podem inibir o crescimento das plantas caso o manejo do solo não seja adequado.
- Umidade do Solo - a água é fator importante no processo de absorção de nutrientes pela planta.
- Material de Origem - Tem relação direta com o tipo e com os teores dos elementos minerais no solo liberados pelo intemperismo. Assim, a composição mineralógica determina maior ou menor disponibilidade de elementos essenciais para as plantas.
- PH do Solo - Grande parte dos solos agrícolas das regiões tropicais e subtropicais apresenta limitações ao crescimento de mutas culturas em virtude dos efeitos da acidez excessiva, que contribui para a baixa fertilidade natural . O PH é o fator que mais afeta a composição da solução do solo.
- Teor de Matéria Orgânica - Produzida pela decomposição de restos vegetais e animais, os compostos orgânicos atuam direta e indiretamente sobre a fertilidade do solo. É fonte de nutrientes para as plantas (N, S, P), aumenta a CTC do solo por contribuir com cargas negativas e regula a disponibilidade de vários micronutrientes, como cobre, manganês e zinco, bem como a atividade de metais pesados e elementos fitotóxicos.
MACRONUTRIENTES
Nutrientes são elementos que ocorrem em maiores concentrações nas plantas, e incluem carbono, hidrogênio, fósforo, potássio, cálcio, magnésio e enxofre. O carbono, o hidrogênio são obtidos da atmosfera; os outros macronutrientes essenciais devem ser obtidos do solo. Desses, o nitrogênio, o fósforo e o potássio são os mais facilmente perdidos no solo e geralmente, são adicionados como fertilizantes. A composição química dos solos é bastante variável, entretanto é possível estimar as porcentagens médias em que os macronutrientes normalmente ocorrem.
CÁLCIO
Solos deficientes em cálcio são relativamente incomuns, pois este constitui o quinto elemento em abundância na crosta terrestre (3,6%) . É encontrado em calcita, gesso, conchas de ostras e corais, e os minerais primários ricos em cálcio são a anortita e os piroxênios.
A aplicação de calcário em solos ácidos fornece cálcio adequadamente para as plantas. No entanto, a absorção de cálcio pelas plantas e a lixiviação por ácido carbônico pode levar à deficiência de cálcio no solo. Solos ácidos podem ainda conter um nível apreciável de cálcio que, devido à concorrência do íon hidrogênio, não esta disponível para as plantas. Em solos alcalinos, a presença de elevados níveis de sódio, magnésio, potássio e cálcio, por vezes, produz deficiência de cálcio, pois esses íons podem competir com o cálcio pela disponibilidade às plantas.
O cálcio é absorvido pelas plantas na forma iônica Ca2+ e transportado para as folhas, nas quais se torna imóvel na forma não solúvel em água. É um elemento que influi indiretamente no rendimento das culturas, por melhorar as condições de crescimento das raízes, estimular a atividade microbiana, auxiliar na disponibilidade do micronutriente molibdênio (Mo) e na absorção de outros nutrientes, além de reduzir o NO3 - na planta. Não há relatos de toxidez por Ca na planta, e o sintoma de deficiência mais comum é o pequeno crescimento das raízes.
NITROGÊNIO
A matéria orgânica é uma importante fonte de nitrogênio no solo, por isso seu ciclo encontra -se ligado à introdução de resíduos orgânicos de origem animal ou vegetal, que, ao sofrerem decomposição pelos micro -organismos, liberam nitrogênio para a solução do solo e, a partir daí, podem ser utilizados por plantas em crescimento. Este processo de decomposição da matéria orgânica é um processo acidificante do solo, pelo qual se forma nitrito (NO2 -) altamente tóxico para as plantas. O nitrito tem vida curta no sol, transformando -se rapidamente em nitrato (NO3-) na presença de oxigênio e do micro-organismo Nitrobacer sp.
O QUE SÃO RIZÓBIOS ?
Os rizóbios são bactérias benéficas presentes no solo que são atraídas para as raízes das plantas leguminosas, ou seja, aquelas que produzem vagens, como o feijoeiro e a soja. Essas bactérias, uma vez em contato com as raízes do feijoeiro, por exemplo, induzem a formação de pequenas bolinhas, chamadas de nódulos. No interior do ar por essas bactérias. Esse processo de aproveitamento do nitrogênio, e permite que o agricultor economize na adubação nitrogenada. O nitrogênio é um dos nutrientes essenciais para o desenvolvimento das plantas e, normalmente, é fornecido para as culturas por meio da adubação com ureia, sulfato de amônia, esterco ou outras formulações do tipo NPK. No entanto, o ar que respiramos contém quase 80% de nitrogênio, na forma de gás, esse pode ser aproveitado pelas plantas por meio do trabalho dos rizóbios, que absorvem esse elemento do ar, transformando -o em aminoácidos ou outros compostos que podem ser utilizados na nutrição nitrogenada do vegetal. Esta associação do rizóbio com as raízes das leguminosas é chamada de simbiose. O rizóbio utiliza os carboidratos provenientes da fotossíntese da planta hospedeira para gerar a energia necessária para promover o processo de fixação biológica de nitrogênio. Por outro lado, a planta beneficia -se do nitrogênio fixado pela bactéria na síntese de suas proteínas.
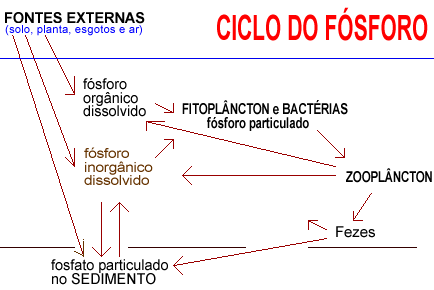
FÓSFORO
O fósforo (P) é essencial para o crescimento e desenvolvimento dos organismos vivos. Em sistemas agrícolas, a adubação com fósforo nos solos, geralmente, é necessária para a reconstituição do fósforo nos solos, geralmente, é necessária para a reconstituição do fósforo removido pelas culturas colhidas ou perdido pela erosão do solo ou pela erosão. As perdas de fósforo são, em geral, significativas no ambiente solo, pois pode aumentar o crescimento de algas e plantas aquáticas a níveis indesejáveis, causando eutrofização de cursos de água.
A concentração de fósforo na solução do solo é amplamente controlada pela mineralização e imobilização do fósforo orgânico compreende entre 30 e 65% do total de fósforo no solo, dependendo do tipo de solo, e inclui ésteres fosfatos, ácidos nucleicos, fosfolipídios e outros ésteres.
VOCÊ SABIA !
O antagonismo pode ser definido como o efeito contrário produzido por um elemento sobre o outro. Exemplo: quando a presença de um elemento no meio diminui a absorção de outro, como no caso do cálcio e do cobre. Normalmente, o antagonismo entre nutrientes -macro e micro causa o surgimento de sintomas de deficiência no nutriente exigido em menores quantidades. Portanto, a deficiencia que deve surgir será a do micronutriente.
Já o sinergismo ocorre quando a presença de um nutriente aumenta a absorção de outro. Exemplo: o magnésio aumenta a absorção do fósforo.