1) Determinar a, de modo que o ângulo A do triangulo ABC, seja 60°. Dados A(1,0,2) B(3,1,3) e C(a+1,-2,3)
Resolução:
AB= B-A= (2,1,1)
AC= C-A= (A,-2,1)
<AB, AC> = (2,1,1) . (a,-2,1) = 2a, -2, +1
<AB, AC> = 2a-1
2) Sejam os vetores a= (1,-m,-3) b= (m+3,4-m,1) e c= m,-2,7) determine m para que a.b= (a+b) . c
Resolução:
a= (1,m,-3)
b= (m+3,4-m,1)
c= (m,-2,7)
a.b = (a+b).c
a.b =
a+b = (1, -m, -3)+(m+3, 4-m,1)
a+b = (m + 4,4 -2m, -2) . (m-2, 7)
(a + b).c = m² + 4m -8+ 4m -14
= -3m+ m² = m² + 8m -22
= -3m - 8m = -22
= -11m = -22
m = -22 / -11
m= 2 //
6) O vetor U= (-1,-1,-2) e V= (2,-3,4) calcular:
a) A área do paralelogramo determinado por U e V
b) A altura do paralelogramo relativa à base definida pelo vetor U
Resolução:
A= |U x V| = i j k
1 -1 1 Determinante= -i -2j - k
2 -3 4
b)
A= b . h
A= raiz de 6
b= raiz de 3
h= ?
10) Determine a altura do tetraedro ABCD, onde A= (1,3,1) B=(0,-2,4) C= (2,1,-3) e D= (0,-6,0).
Resolução:
AB= B-A= (-1,-5,3)
AC= C-A= (1-2,-4)
AD= D-A= (-1,-9,-1)
-1 -5 3
1 -2 -4
-1 -9 -1
Determinante = -24 = 24
Volume = Ab . h / 2
V = (1/6) . 24
V= 4u
h= ?
v= 4
Ab= raiz de 726
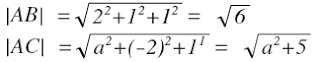
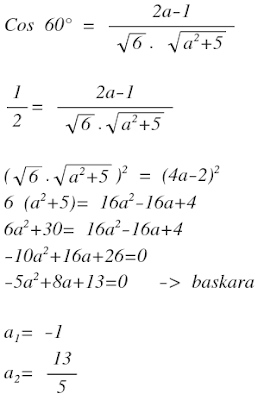
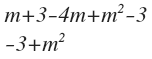



Nenhum comentário:
Postar um comentário