Resistencia dos Materiais "6-82 , 6-83 "

6-82) Se o feixe em Prov. 6-23 tem uma secção transversal como mostrado, determine a curvatura máxima absoluta estresse no feixe.

- 30 * 1,5 * (0,75 + 3) - 30 * 1,5 * 0,75 + 30 + Ra * 3 = 0
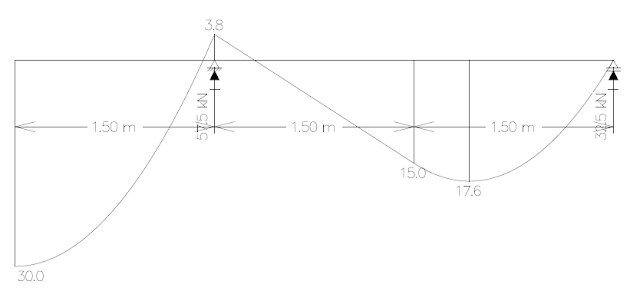
Ra = 57,5 KN

Rb + 57,5 - 30 * 1,5 - 30 * 1,5 = 0
Rb = 32,5 KN

Mmax = 30KN.m

Ix = 21839616 mm⁴

σmax = (σf / Ix) . y
σmax = (30X10⁶ N.mm . 96mm) / 21839616 mm⁴
σmax = 131,87 MPa

6-83) O pino é usada para ligar as três ligações em conjunto. Devido ao desgaste, a carga é distribuída ao longo do topo e parte inferior do pino, como mostrado no diagrama de corpo livre. Se o diâmetro do pino é de 10 mm, de determine tensão máxima de flexão sobre a área da seção transversal na aa seção central. Para a solução é primeiro necessário determinar as intensidades de carga e w1 w2.

∑Ma =0
2 . (25 / 3 + 37,5  / 2) - 2 .( 37,5 /2) + Ma = 0
Ma = - 16666,7 N.mm

Ix = π . R⁴  . 1/4

Ix = (π . 5⁴ ) / 4 = 490,8738 mm⁴

Cg = 10 /2 = 5 mm