1) Você esta a deriva no espaço, afastado de sua nave espacial. Por sorte você tem uma unidade de propulsão que fornece uma força resultante constante F por 3s. Apos 3s você se moveu 2,25m. Se sua massa é 68 Kg, encontre F.
RESOLUÇÃO
2,25 = 0,5 * a * 32
a= 2,25 /4,5
a= 0,5 m/s2
FR= m * a
FR= 68 * 0,5
FR = 34 N
2) Durante as férias de inverno você participa de uma corrida de trenos em que estudantes substituem os cães calçando botas de neve com travas que permitem uma boa tração, você começa a corrida puxando uma corda atada ao trenó com uma força de 150 N a 25° acima da horizontal. A partícula treno - passageiro corda tem uma massa de 80 Kg e não existe atrito entre as laminas do treno e o gelo. Encontre
a) a aceleração do treno e
b) a magnitude da força normal exercida pela superfície sobre o treno
RESOLUÇÃO
a)
Fx = m *a
150 * cos 25 = 80 * a
a= 1,7 m/s2
b)
Na + Fy - Fg = 0
Na= Fg - Fy
Na = (m * g ) - Fy
Na= 80 * 9,8 - 63,4
Na= 720,6 N
3) Um bloco desliza para baixo em um plano sem atrito com uma inclinação de 15°. O bloco parte do repouso no topo e o comprimento da rampa é de 2m. Encontre
a) a aceleração do bloco
b) sua velocidade quando ele atinge a parte inferior da rampa
RESOLUÇÃO
a)
a = g * sen 15°
a = 2,54 m/s2
b)
V2 = 02 + 2 * 2,54 * 2
V= 3,19 m/s
5) Uma caixa de 20 Kg está sobre uma rampa sem atrito inclinada de 15°. Alguém puxa a caixa para cima com uma corda. Se a corda forma uma angulo de 40° com a horizontal, qual é a menor força força F capaz de deslocar a caixa rampa acima ?
RESOLUÇÃO
40° - 25° = 15°
F= ( m * g * sen 15° ) / cos 25°
F = ( 20 * 9,8 * sen 15° ) / cos 25°
F = 56 N
6) Três caixas são conectadas por cordas, uma das quais passa por uma polia de atrito e massa desprezíveis. As massas são ma = 30 Kg, mb = 40 Kg, mc = 10 Kg. Quando o conjunto é liberado a partir do repouso.
a) qual é a tensão da corda que liga B a C
b) que distancia A percorre nos primeiros 0,25s (supondo que não atinge a polia)
RESOLUÇÃO
a)
T =
ma * a
T + Pb - T =
mb * a
Pc - T = mc * a
+
Pb + Pc = (ma + mb + mc ) a
490 = 80 * a
a= 6,12 m/s2
b)
X = X0 + 0,5 * a * t
X = 0,5 (6,12 * 0,252 )
X = 0,19 m
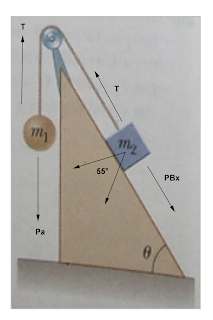
7) Dois corpos são conectados por uma corda leve que passa sobre uma polia sem atrito, como mostra a figura. Considere que a rampa seja sem atrito e m1 = 2 Kg, m2 = 6 Kg e
θ = 55°.
a) Encontre o modulo da aceleração dos corpos
b) A tensão na corda
c) A velocidade de cada corpo depois de 2s de ter sido liberado do repouso
RESOLUÇÃO
Pa= 19,6 N
Pb= 58,8 N
Pbx = 58,8 *sen 55° = 48,16 N
Pby= 58,8 * cos 55° = 33,72 N
a)
T - Pa = m1 * a
- T + Pbx = m2 * a
+
- Pa + Pbx = ( m1 + m2 ) * a
-19,6 + 48,16 = (2 + 6) a
a= 3,57 m/s2
b)
T - Pa = m1 * a
T = 19,6 + ( 2 * 3,57)
T = 26,74 N
c)
V = ( 3,57 * 2
2 ) / 2
V = 7,14 m/s
8) Em um jogo de shuffeboard improvisado, estudantes enlouquecidos pelos exames finais usam uma vassoura para movimentar um livro de cálculo no corredor do dormitório. Se o livro de 3,5 Kg adquire uma velocidade de 1,6 m/s ao ser empurrado pela vassoura a partir do repouso com uma forca horizontal de 25 N, por uma distancia de 0,9m, qual é o coeficiente de atrito cinético entre o livro e o piso ?
RESOLUÇÃO
µc = (25 / 3,5 - (1,62 / 2 * 9,8)) / 9,8
µc = 0,58
9) Você depõe como perito em um caso envolvendo um acidente no qual um carro A bateu na traseira de um carro B que estava parado em um sinal vermelho no meio de uma ladeira. Você descobre que a inclinação da ladeira θ= 12°e que os carros estavam separados por uma distancia d= 20m quando o motorista do carro A freou bruscamente, travando as rodas (o carro não dispunha de freios ABS) , e que a velocidade do carro A no momento em que o motorista pisou no freio era V0= 18 m/s.
a) Com que velocidade o carro A bateu no carro B se o coeficiente de atrito cinético era 0,6 (estrada seca)
b) 0,1 (estrada coberta de folhas molhadas) ?
RESOLUÇÃO
FR = m * a
m * g * sen θ - µc * Fn = m * a (Fn = m* g * cos θ)
m * g * sen θ - µc * m * g * cos θ = m * a
a = g (sen θ - µc * cos θ )
a)
a= 9,8 (0,6 * cos 12 - sen 12°)
a = 3,71 m/s2
V2 = 182 - 2 * 3,71 * 24
V= 12,08 m/s
b)
PISTA MOLHADA
a = 9,8 (0,1 * cos 12° - sen 12° )
a = 1,08 m/s2
V2 = 182 - 2 (-1,08 * 24)
V= 19,4 m/s
10) Um disco de metal de massa m= 1,5 Kg descreve uma circunferência de raio r= 20 cm sobre uma mesa sem atrito, enquanto permanece ligado a um cilindro de massa m= 2,5 Kg pendurado por um fio que passa por um furo no centro da mesa. Que velocidade do disco mantém o cilindro em repouso ?
RESOLUÇÃO
Fc = m * V2 * r
Fc = P
1,5 * V2 * (20 / 100) = 2,5 * 9,8
V = 9,04 rad / s
V = 9,04 *(20 / 100)
V = 1,81 m/s
11) Uma pessoa empurra horizontalmente um caixote de 55 Kg com uma força de 220 N para deslocá -lo em um piso plano. O coeficiente de atrito cinético é 0,35.
a) Qual é o módulo da força de atrito ?
b) Qual é o módulo da aceleração do caixote ?
RESOLUÇÃO
a)
Fat = µc * FN
Fat = 0,35 * 55 * 9,8
Fat = 188,65 N
b)
F - Fat = FR
220 - 188,65 = 55 * a
a = 0,57 m/s2
12) Uma partícula de 0,4 Kg de massa está submetida simultaneamente a duas forças, F1 = (-2i , 4j ) e F2 = ( -2,6i , 5j ). Se a partícula está na origem e parte do repouso em t = 0s . Encontre
a) sua posição R
b) sua velocidade V em t = 1,6s
RESOLUÇÃO
∑ F = (-4,6 , 1)
a= F / m
a= (-4,6 / 0,4)i , (1 / 0,4)j
a = (-11.5 ; 2,5)
V = V + a * t
Vx = 0 -11,5 * 1,6
Vx = -18,4 m/s
Vy = 0 + 2,5 * 1,6
Vy = 4 m/s
V = (-18.4 ; 4)
R= R0 + V0 * t * 0,5 * a * t2
Rx = 0,5 * (-11,5 * 1,62)
Rx = -14,7
Ry = 0,5 * (2,5 * 1,62)
Ry = 3,2
R= (-14.7 ; 3,2)
13) Um livro de dura está sobre uma mesa com uma capa virada para cima. Você coloca uma moeda sobre esta capa e, muito lentamente abre o livro até que a moeda comece a escorregar. O ângulo θmax (conhecido como angulo de repouso) é o angulo que a capa forma com a horizontal justo quando a moeda começa a escorregar. Encontre o coeficiente de atrito estático µ, entre a capa do livro e a moeda, em termos de θmax.
RESOLUÇÃO
fc= Px
µe * Fx = P * sen θ
µe = ( P * sen θ ) / P * cos θ
µe = (sen θ) / cos θ
µe = = Tg θ
14) Um elevador e sua carga possuem massa total de 800 Kg. O elevador está inicialmente descendo com velocidade de 10 m/s; a seguir ele atinge o repouso em uma distancia de 25m. Ache a tensão no cabo de suporte enquanto está diminuindo de velocidade até parar.
RESOLUÇÃO
V2 = V02 + 2 * a * Δx
02 = (-102) + 2 * a * (-2,5)
a = 2 m/s2
- P + T = m * a
T = 7840 + (800 * 2)
T = 9440 N
15) Na figura um caixote de massa m= 100 Kg é empurrado por uma força horizontal F que o faz subir uma rampa sem atrito (θ =30°) com velocidade constante. Quais são os módulos de:
a) F
b) da força que a rampa exerce sobre o caixote ?
RESOLUÇÃO
a)
Fx = Px
F * cos 30° = P * sen 30°
F = (980 * sen 30°) / cos 30°
F = 565,8 N
b)
FN = Py + Fy
FN = P * cos 30° + F * sen 30°
FN = 980 * cos 30° + 565,8 * sen 30°
FN = 1131,6 N
16) A figura mostra um arranjo no qual 4 discos estão suspensos por cordas. A corda mais comprida no alto, passa por uma polia sem atrito e exerce uma força de 98 N sobre a parede à qual está presa. As tensões nas cordas mais curtas são T1 = 58,8 N, T2 = 49 N e T3 = 9,8. Quais são são as massas:
a) do disco A
b) do disco B
c) do disco C
d) do disco D
RESOLUÇÃO
T1 = 58,8 N
T2 = 49 N
T3 = 9,8 N
FR = 0
T3 - Pd = 0
9,8 = Pd
m * g = 9,8
md = 1 Kg
T2 - T3 - Pc = 0
- Pc = -39,2
Pc = 39,2 N
mc * g = 39,2
mc = 4 Kg
T1 - T2 - Pb = 0
58,8 - 49 - Pb = 0
- Pb = -9,8
Pb = 9,8 N
mb * g = 9,8
mb = 1 Kg
T - T1 - Pa = 0
9,8 - 58,8 - ma * g = 0
39,2 = ma * g
ma = 4 Kg
17) A figura mostra dois blocos ligados por uma corda (de massa desprezível) que passa por uma polia sem atrito (também de massa desprezível). O conjunto é conhecido como máquina de Atwood. Um bloco tem m1 = 1,3 Kg: o outro tem massa m2 = 2,8 Kg. Quais são :
a) o módulo da aceleração dos blocos ?
b) a tensão na corda ?
RESOLUÇÃO
P2 - T = m2 * a
- P1 + T = m1 * a
+
P2 - P1 = (m1 + m2 ) a
27,47 - 12,75 = 1,3 +2,8 * a
a = 3,59 m/s2
- P1 + T = m1 * a
T = 12,74 + (1,3 * 3,59)
T = 17,4 N
18) A figura mostra tres blocos ligados por cordas que passam por polias sem atrito. O bloco B está sobre uma mesa sem atrito; as massas são mA = 6 Kg , mB = 8 kG e mC = 10 Kg. Quando os blocos são liberados qual é a tensão da corda da direita ?
RESOLUÇÃO
Pc - T = mC * a
- Pa + T = mA * a
T - T = mB * a
+
Pc - Pa = (mC + mA + mB) *a
98 - 58,8 = (10 + 6+ 8) * a
a = 1,6333 m/s2
Pc - T = mC * a
- T = - Pc + (mC * a) (-1)
T = 98 - (10 * 1,6333)
T = 81,67 N
19) O bloco 1, de massa m1 = 2 Kg e o bloco 2, de massa m2 = 3 Kg estão ligados por um fio de massa desprezível e são inicialmente mantidos em repouso. O bloco 2 está sobre uma superfície sem atrito com uma inclinação θ =30°. O coeficiente de atrito cinético entre o bloco 1 e a superfície horizontal é de 0,25. A polia tem massa e atrito desprezíveis. Uma vez soltos, os blocos entram em movimento. Qual é a tensão do fio ?
RESOLUÇÃO
P2 - T = m2 * a
P2 * sen θ - T = m2 * a
- T = - 14,7 + (3 * a )
T = 14,7 - 3 * a
9,8 = 5 * a
a = 1,96 m/s2
T - fat = m1 * a
T = (2 * 9,8 * 0,25 ) 2 *a
T = 4,9 + 2 * a
T = 4,9 + 2 * 1,96
T = 8,82 N